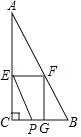题目内容
【题目】已知直角△ABC中，∠C=90°，BC=3，AC=4，那么它的内切圆半径为_______.
【答案】1
【解析】
分别与BC、AC、AB切于点D、E、F，连接OD、OE、OF，由切线的性质可得：∠ODC=∠OEC=90°，设OD=OE=r根据正方形的判定即可证出四边形OECD是正方形，从而得出：EC=CD=OD=OE=r，再根据切线长定理可得：BF=BD =3－r，AF=AE =4－r，再根据勾股定理求出AB，利用AB的长列方程即可.
解：如图所示，分别与BC、AC、AB切于点D、E、F，连接OD、OE、OF
∴∠ODC=∠OEC=90°
∵∠C=90°，设OD=OE=r
∴四边形OECD是正方形
∴EC=CD=OD=OE=r
根据切线长定理可得：BF=BD=BC－CD=3－r，AF=AE=AC－EC=4－r
由勾股定理可知：AB=
∵AF＋BF=AB
∴（4－r）＋（3－r）=5
解得：r=1
故答案为：1
练习册系列答案
相关题目
【题目】2017年的淘宝双十一，开场11秒后，销售额突破十亿，3分钟破百亿，最终成交额定格在1682亿元上，在今年的双十一前夕，某企业生产一种必需商品作为双十一的主打商品，经过之前的长期市场调查后发现，商品的月总产量稳定在600件，商品的月销售量a（件）由固定销售量与浮动销售量两个部分组成，其中固定销售量保持不变，浮动销售量与售价x（元/件）（x≤10）成反比，且得到了如下表格中的信息：
售价x（元/件） | 5 | 8 |
月销售量Q（件） | 580 | 400 |
（1）求Q关于x的函数关系式；
（2）若生产的所有商品正好销售完，求售价x；
（3）求售价x为多少时，月销售额最大，并求这个最大值．
