Question

【题目】如图，利用函数y＝x2﹣4x+3的图象，直接回答：

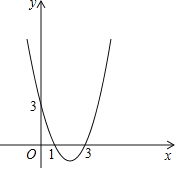
（1）方程x2﹣4x+3＝0的解是　 　；

（2）当x满足　 　时，函数值大于0．

（3）当0＜x＜5时，y的取值范围是　 　．

Answer 1

【答案】（1）x1＝1，x2＝3；（2）x＜1或x＞3；（3）﹣1≤y＜8．

【解析】

（1）根据方程x2﹣4x+3＝0的解就是抛物线与x轴交点的横坐标可得答案；

（2）结合函数图象写出抛物线在x轴上方所对应的自变量的范围即可；

（3）先分别计算出x＝0和x＝5对应的函数值，再利用配方法得到当x＝2时，y有最小值﹣1，然后结合函数图象求解．

（1）∵抛物线与x轴的交点坐标为（1，0），（3，0），

∴方程x2﹣4x+3＝0的解是x1＝1，x2＝3；

（2）由函数图象可知：当x＜1或x＞3时，y＞0；

（3）当x＝0时，y＝x2﹣4x+3＝3；当x＝5时，y＝x2﹣4x+3＝25﹣20+3＝8，

∵y＝x2﹣4x+3＝（x﹣2）2﹣1，

∴当x＝2时，y有最小值﹣1，

∴当0＜x＜5时，y的取值范围为﹣1≤y＜8．