Question

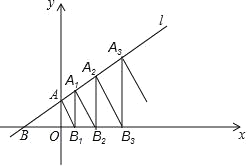
【题目】如图，在平面直角坐标系中，点A，A1，A2，A3…An都在直线1：y＝x+1上，点B，B1，B2，B3…Bn都在x轴上，且AB1⊥1，B1A1⊥x轴，A1B2⊥1，B2A2⊥x轴，则An的横坐标为_________（用含有n的代数式表示）。

Answer 1

【答案】（()n﹣1）

【解析】

根据题意：先求出AO，A1B1，A2B2的长度，找出规律，表示出AnBn，再计算OBn，可得An的横坐标．

∵直线1：y＝x+1交x轴，y轴于B，A两点

∴A（0，1），B（﹣，0）

∵AB1⊥1，B1A1⊥x轴，A1B2⊥1，B2A2⊥x轴

∴A1B1∥AO∥A2B2∥A3B3，AB1∥A1B2∥A2B3．

∴∠B＝∠OAB1＝∠B1A1B2＝∠B2A2B3．

∴tan∠B＝tan∠OAB1＝

∴OB1＝

∵OA∥A1B1

∴

∴A1B1＝

同理可得A2B2＝

…AnBn＝()n

∵OB1＝AO×tan∠OAB1＝1×＝

∴B1B2＝A1B1×tan∠OAB1＝×

…An﹣1Bn＝An﹣1Bn﹣1×tan∠OAB1＝()n-1×

∴OBn＝OB1+B1B2+B2B3+…+An﹣1Bn﹣1＝+×+()2×+…+()n-1×①

∴OBn＝ +()2×+…+()n-1×+()n×②

∴②﹣①得OBn＝()n ×﹣

∴OBn＝（()n﹣1）

故答案为（()n﹣1）