题目内容
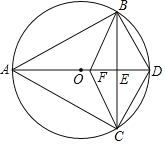
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
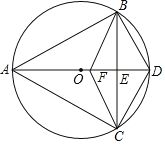
(1)求证:BE=CE;
(2)若BC=8,AD=10,求四边形BFCD的面积.
【答案】(1)见解析;(2)四边形BFCD的面积为16.
【解析】
(1)由AB=AC可得![]() ,然后根据垂径定理的推论即可证得结论;
,然后根据垂径定理的推论即可证得结论;
(2)先根据ASA证得△BED≌△CEF,从而可得CF=BD,于是可推得四边形BFCD是平行四边形,进一步即得四边形BFCD是菱形;易证△AEC∽△CED,设DE=x,根据相似三角形的性质可得关于x的方程,解方程即可求出x的值,再根据菱形面积公式计算即可.
(1)证明:∵AB=AC,∴![]() ,
,
∵AE过圆心O,∴BE=CE;
(2)解:∵AB=AC,BE=CE,∴AD⊥BC,∠BAD=∠CAD,∴∠BED=∠CEF=90°,
∵CF∥BD,∴∠DBE=∠FCE,
∴△BED≌△CEF(ASA),∴CF=BD,
∴四边形BFCD是平行四边形,
∵AD⊥BC,∴平行四边形BFCD是菱形;
∴BD=CD,∴![]() ,∴∠CAE=∠ECD,∵∠AEC=∠CED=90°,
,∴∠CAE=∠ECD,∵∠AEC=∠CED=90°,
∴△AEC∽△CED,∴![]() ,∴CE2=DEAE,
,∴CE2=DEAE,
设DE=x,∵BC=8,AD=10,∴CE=4,AE=10-x,
∴42=x(10﹣x),解得:x=2或x=8(舍去),
∴DF=2DE=4,
∴四边形BFCD的面积=![]() ×4×8=16.
×4×8=16.

【题目】汽车刹车后,还会继续向前滑行一段距离,这段距离称为“刹车距离”刹车距离y(m)与刹车时的车速x(km/h)的部分关系如表:
刹车时的车速 | 0 | 50 | 100 | 150 | 200 |
刹车距离 | 0 | 5.5 | 21 | 46.5 | 82 |
(1)求出y与x之间的函数关系式.
(2)一辆车在限速120km/h的高速公路上行驶时出了事故,事后测得它的刹车距离为40.6m,问:该车在发生事故时是否超速行驶?