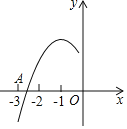题目内容
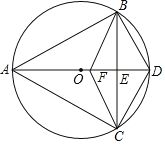
【题目】如图,BD是平行四边形ABCD的对角线,DE⊥AB于点E,过点E的直线交BC于点G,且BG=CG.
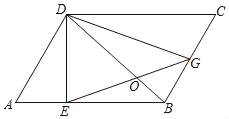
(1)求证:GD=EG.
(2)若BD⊥EG垂足为O,BO=2,DO=4,画出图形并求出四边形ABCD的面积.
(3)在(2)的条件下,以O为旋转中心顺时针旋转△GDO,得到△G′D'O,点G′落在BC上时,请直接写出G′E的长.
【答案】(1)详见解析;(2)图详见解析,12![]() ;(3)
;(3)![]() .
.
【解析】
(1)如图1,延长EG交DC的延长线于点H,由“AAS”可证△CGH≌△BGE,可得GE=GH,由直角三角形的性质可得DG=EG=GH;
(2)通过证明△DEO∽△DBO,可得![]() ,可求DE=
,可求DE=![]() ,由平行线分线段成比例可求EG=
,由平行线分线段成比例可求EG=![]() ,GO=EG-EO=
,GO=EG-EO=![]() ,由勾股定理可求BG=CG=
,由勾股定理可求BG=CG=![]() ,可得DE=AD,即点A与点E重合,可画出图形,由面积公式可求解;
,可得DE=AD,即点A与点E重合,可画出图形,由面积公式可求解;
(3)如图3,过点O作OF⊥BC,由旋转的性质和等腰三角形的性质可得GF=G'F,由平行线分线段成比例可求GF的长,由勾股定理可求解.
证明:(1)如图1,延长EG交DC的延长线于点H,
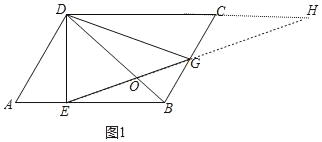
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,AB=CD,AB∥CD,
∵AB∥CD,
∴∠H=GEB,又∵BG=CG,∠BGE=∠CGH,
∴△CGH≌△BGE(AAS),
∴GE=GH,
∵DE⊥AB,DC∥AB,
∴DC⊥DE,
∴DG=EG=GH;
(2)如图1:∵DB⊥EG,
∴∠DOE=∠DEB=90°,且∠EDB=∠EDO,
∴△DEO∽△DBO,
∴![]() ,
,
∴DE×DE=4×(2+4)=24,
∴DE=![]()
∴EO=![]() ,
,
∵AB∥CD,
∴![]() ,
,
∴HO=2EO=![]() ,
,
∴EH=![]() ,且EG=GH,
,且EG=GH,
∴EG=![]() ,GO=EG﹣EO=
,GO=EG﹣EO=![]() ,
,
∴GB=![]() ,
,
∴BC=![]() =AD,
=AD,
∴AD=DE,
∴点E与点A重合,
如图2:
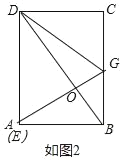
∵S四边形ABCD=2S△ABD,
∴S四边形ABCD=2×![]() ×BD×AO=6×2
×BD×AO=6×2![]() =12
=12![]() ;
;
(3)如图3,过点O作OF⊥BC,
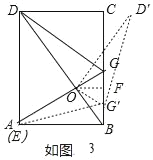
∵旋转△GDO,得到△G′D'O,
∴OG=OG',且OF⊥BC,
∴GF=G'F,
∵OF∥AB,
∴![]() ,
,
∴GF=![]() BG=
BG=![]() ,
,
∴GG'=2GF=![]() ,
,
∴BG'=BG﹣GG'=![]() ,
,
∵AB2=AO2+BO2=12,
∵EG'=AG'=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如下表格:
的图象可以得到如下表格:
|
|
|
|
|
|
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可得到如下表格:
的图象可得到如下表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() 的图象;
的图象;
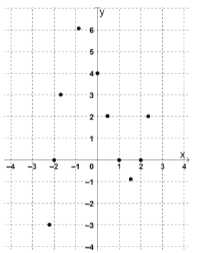
观察函数![]() 的图象,
的图象,
补全下面的表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法,解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .