题目内容
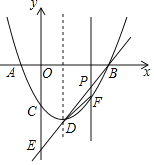
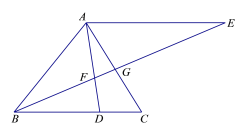
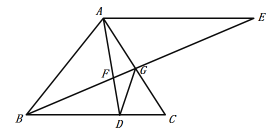
【题目】已知：如图，在△ABC中，点D在边BC上，AE∥BC，BE与AD、AC分别相交于点F、G， 
．
（1）求证：△CAD∽△CBG；
（2）联结DG，求证：
．
【答案】（1）见解析；（2）见解析；
【解析】
（1）由
及∠AFG=∠EFA，证得△FAG∽△FEA，结合AE∥BC，证得∠EBC =∠FAG，从证得结论；
（2）由（1）的结论得到
，证得△CDG ∽△CAB，结合AE∥BC，证得
，继而证得结论.
（1）∵，
∴
．
又∵∠AFG=∠EFA，
∴△FAG∽△FEA．
∴∠FAG=∠E．
∵AE∥BC，
∴∠E=∠EBC．
∴∠EBC =∠FAG．
又∵∠ACD=∠BCG，
∴△CAD ∽△CBG．
（2）∵△CAD ∽△CBG，
∴．
又∵∠DCG=∠ACB，
∴△CDG ∽△CAB，
∴
．
∵AE∥BC，
∴
．
∴，
∴
，
∴
．
练习册系列答案
相关题目
