题目内容
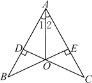
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点M,MN⊥AC于点N. 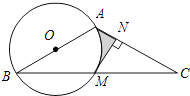
(1)求证:MN是⊙O的切线;
(2)若∠BAC=120°,AB=2,求图中阴影部分的面积.
【答案】
(1)解:证明:连接OM.
∵OM=OB,
∴∠B=∠OMB.
∵AB=AC,
∴∠B=∠C.
∴∠OMB=∠C.
∴OM∥AC.
∵MN⊥AC,
∴OM⊥MN.
∵点M在⊙O上,
∴MN是⊙O的切线

(2)解:连接AM.
∵AB为直径,点M在⊙O上,
∴∠AMB=90°.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∴∠AOM=60°.
又∵在Rt△AMC中,MN⊥AC于点N,
∴∠AMN=30°.
∴AN=AMsin∠AMN=ACsin30°sin30°= ![]() .
.
∴MN=AMcos∠AMN=ACsin30°cos30°= ![]() .
.
∴S梯形ANMO= ![]() ,
,
S扇形OAM= ![]() ,
,
∴S阴影= ![]() =
= ![]() ﹣
﹣ ![]() .
.
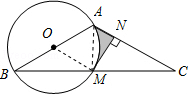
【解析】(1)有切点,需连半径,证明垂直,即可;(2)求阴影部分的面积要把它转化成S梯形ANMO﹣S扇形OAM , 再分别求的这两部分的面积求解.
【考点精析】掌握切线的判定定理和扇形面积计算公式是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

 习题精选系列答案
习题精选系列答案【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年度 | 投入技改资金 | 产品成本 |
2014 |
|
|
2015 | 3 | 12 |
2016 | 4 | 9 |
2017 |
| 8 |
(1)分析表中数据,请从一次函数和反比例函数中确定一个函数表示其变化规律,直接写出y与x的函数关系式;
(2)按照这种变化规律,若2018年已投入资金6万元.
①预计2018年每件产品成本比2017年降低多少万元?
②若计划在2018年把每件产品成本降低到5万元,则还需要投入技改资金多少万元?