题目内容
【题目】如图,直线l1的解析式为y=-x+4,直线l2的解析式为y=x-2,l1和l2的交点为点B.

(1)直接写出点B坐标;
(2)平行于y轴的直线交x轴于点M,交直线l1于E,交直线l2于F.
①分别求出当x =2和x =4时E F的值.
②直接写出线段E F的长y与x的函数关系式,并画出函数图像L.
③在②的条件下,如果直线y=kx+b与L只有一个公共点,直接写出k的取值范围.
【答案】(1)(3,1);(2)①EF=2;②见解析. ③k >2或k<-2或.k=-![]()
【解析】(1)直接联立两个解析式求解即为点B的坐标.
(2)①当x=2时,分别求出点E、F的纵坐标即可解答.
当x=4时,分别求出点E、F的纵坐标即可解答.
②分两种情况讨论:当x![]() 或x
或x![]() 时,线段E F的长y与x的函数关系式.
时,线段E F的长y与x的函数关系式.
(1)联立两个解析式可得y=-x+4y=x-2,
解得x=3,y=1,∴点B的坐标为(3,1);
(2)①如图:
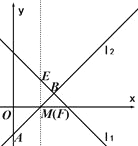
当x=2时,y=-x+4=2,∴E(2,2),
当x=2时,y=x-2=0,∴F(2,0),
∴EF=2;
如图:
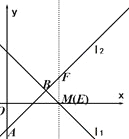
当x=4时,y=-x+4=0,∴E(4,0),
当x=4时,y=x-2=2,∴F(4,2),
∴EF=2;
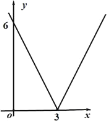
② L:![]() ,
,
图像如图所示:
③k >2或k<-2或.k=-![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目









