ЬтФПФкШн
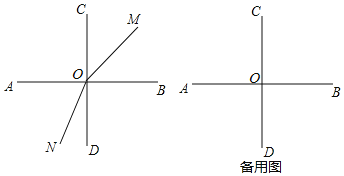
ЁОЬтФПЁПвбжЊЃКЪ§жсЩЯгаAЁЂBЁЂCШ§ИіЕуЃЌЫќУЧБэЪОЕФЪ§ЗжБ№ЪЧaЁЂbКЭ8ЃЌOЪЧдЕуЃЌЧвЃЈa+20ЃЉ2+|b+10|ЃН0ЃЎ
ЃЈ1ЃЉЬюПеЃКaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєНЋЪ§жселЕўЃЌЪЙЕУЕуAгыЕуCжиКЯЃЌдђЕуBгыЪ§ЁЁ ЁЁБэЪОЕФЕужиКЯЃЛ
ЃЈ3ЃЉЖЏЕуMдкЪ§жсЩЯдЫЖЏЃЌЪЧЗёДцдкЕуMЪЙЕУMC+MBЃН20ЃЌШєДцдкЃЌЧыЧѓГіЕуMЖдгІЕФЪ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ4ЃЉЯжгаЖЏЕуPЁЂQЗжБ№ДгAЁЂBСНЕуГіЗЂЃЌЕуPвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуCвЦЖЏЃЌЭЌЪБЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђЕуCвЦЖЏЃЎЩшЕуPвЦЖЏЕФЪБМфЮЊtУыЃЌЮЪЃК
ЂйЕБtЮЊЖрЩйЪБЃЌЕуPзЗЩЯЕуQЃП
ЂкгУКЌtЕФДњЪ§ЪНБэЪОЯпЖЮPQЕФГЄЖШЃП
ЁОД№АИЁПЃЈ1ЃЉЉ20ЃЛЉ10ЃЛЃЈ2ЃЉЉ2ЃЛЃЈ3ЃЉДцдкЕуMЪЙЕУMC+MBЃН20ЃЌЕуMЖдгІЕФЪ§ЮЊЉ11Лђ9ЃЎЃЈ4ЃЉЂйЕБtЮЊ5ЪБЃЌЕуPзЗЩЯЕуQЃЎЂкPQЃН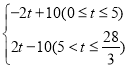 ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦНЗНЪ§ЕФЗЧИКадЁЂОјЖджЕЕФЗЧИКадСаГіЕШЪНЃЌЧѓНтМДПЩЃЛ
ЃЈ2ЃЉгЩелЕўКѓжиКЯЕФЕуБэЪОЕФЪ§жЎКЭВЛБфЃЌЧѓНтМДПЩЕУЃЛ
ЃЈ3ЃЉЩшЕуMЖдгІЕФЪ§ЮЊ![]() ЃЌЗжЕуMдкЕуCЕФгвВрЃЈКЌЕуCЃЉЁЂЕуMдкBЁЂCСНЕужЎМфЃЈКЌЕуBЃЉЁЂЕуMдкЕуBЕФзѓВрШ§жжЧщаЮЃЌИљОн
ЃЌЗжЕуMдкЕуCЕФгвВрЃЈКЌЕуCЃЉЁЂЕуMдкBЁЂCСНЕужЎМфЃЈКЌЕуBЃЉЁЂЕуMдкЕуBЕФзѓВрШ§жжЧщаЮЃЌИљОн![]() СаГіЕШЪНЧѓНтМДПЩЃЛ
СаГіЕШЪНЧѓНтМДПЩЃЛ
ЃЈ4ЃЉИљОнЬтвтЕУЃЌЕуPБэЪОЕФЪ§ЮЊ![]() ЃЌЕуQБэЪОЕФЪ§ЮЊ
ЃЌЕуQБэЪОЕФЪ§ЮЊ![]()
ЂйЕуPзЗЩЯЕуQЃЌдђЕуPБэЪОЕФЪ§ЕШгкЕуQБэЪОЕФЪ§ЃЌСаГіЕШЪНЧѓНтМДПЩЃЛ
ЂкгЩЬтЂйПЩжЊЃЌЕуPзЗЩЯЕуQЪБЃЌЛЙЮДЕНДяЕуCЃЌЫљвдЗжСНжжЧщПіЃКдкЕуPзЗЩЯЕуQжЎЧАЁЂдкЕуPзЗЩЯЕуQжЎКѓжСЕНДяЕуCЃЌЗжБ№РћгУЕуPЁЂQДњБэЕФЪ§зїВюМДПЩ.
ЃЈ1ЃЉ![]()
гЩЦНЗНЪ§ЕФЗЧИКадЁЂОјЖджЕЕФЗЧИКадЕУ
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉгЩелЕўКѓжиКЯЕФЕуБэЪОЕФЪ§жЎКЭВЛБфПЩЕУЃК![]()
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЩшЕуMЖдгІЕФЪ§ЮЊ![]() ЃЌгЩЬтвтЗжвдЯТШ§жжЧщаЮЃК
ЃЌгЩЬтвтЗжвдЯТШ§жжЧщаЮЃК
ЂйЕуMдкЕуCЕФгвВрЃЈКЌЕуCЃЉЃЌДЫЪБ![]()
дђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЗћКЯ
ЃЌЗћКЯ![]() ЕФШЁжЕЗЖЮЇ
ЕФШЁжЕЗЖЮЇ
ЂкЕуMдкBЁЂCСНЕужЎМфЃЈКЌЕуBЃЉЃЌДЫЪБ![]()
дђ![]() ЃЌЗНГЬЮоНт
ЃЌЗНГЬЮоНт
ЂлЕуMдкЕуBЕФзѓВрЃЌДЫЪБ![]()
дђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЗћКЯ
ЃЌЗћКЯ![]() ЕФШЁжЕЗЖЮЇ
ЕФШЁжЕЗЖЮЇ
ЙЪДцдкетбљЕФЕуMЪЙЕУ![]() ЃЌЕуMЖдгІЕФЪ§ЮЊ
ЃЌЕуMЖдгІЕФЪ§ЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ4ЃЉгЩЬтвтЕУЃЌЕуPБэЪОЕФЪ§ЮЊ![]() ЃЌЕуQБэЪОЕФЪ§ЮЊ
ЃЌЕуQБэЪОЕФЪ§ЮЊ![]()
ЂйЕуPзЗЩЯЕуQЃЌдђ![]()
НтЕУЃК![]()
Д№ЃКЕБtЮЊ5ЪБЃЌЕуPзЗЩЯЕуQЃЛ
ЂкгЩЬтвтЕУЃЌЕуPЯШзЗИЯЕуQЃЌзЗЩЯКѓЛсЯШЕНДяЕуC
ЕуPЕНДяЕуCЪБЃЌЕуPвЦЖЏЕФЪБМф![]() ЮЊЃК
ЮЊЃК![]() ЃЌМД
ЃЌМД![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
злЩЯЃЌ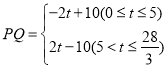 .
.