��Ŀ����
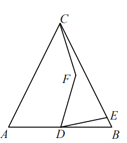
����Ŀ����ABC��һ�麬��45��ֱ�����ǰ壬�ı���DEFG�dz����Σ�D��G�ֱ���AB��AC�ϣ�E��F��BC�ϡ�BC=16,DG=4��DE=6���ֽ������� DEFG������BC����ƽ�ƣ���ˮƽ�ƶ��ľ���Ϊd����������ֱ�����ǰ���ص����ΪS��
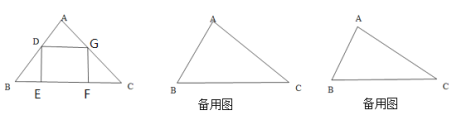
��1����ˮƽ����d�Ǻ�ֵʱ�������� DEFGǡ����ȫ�Ƴ����ǰ壻
��2�����ƶ������У������ú���d�Ĵ���ʽ��ʾ�ص����S����д����Ӧ��d�ķ�Χ��
���𰸡���1��10����2����0<d��4ʱ��S=24-![]() ����4<d��6ʱ��S=32-4d����6<d��10ʱ��S=
����4<d��6ʱ��S=32-4d����6<d��10ʱ��S=![]() ����10<dʱ,S=0.
����10<dʱ,S=0.
��������
��1��Ҫʹ��������ȫ�Ƴ������Eƽ�Ƶ��˵�C������ʱd=EC���ɵ���ֱ�������ε����ʿ�֪��B=45�����Ӷ��õ�BE=DE=6.���ü���BC-BE��ֵ����.
��2��������������λ���ͼ�Σ��ٽ��ͼ�ν��м��㼴��.
�⣺��1������ABC�ǵ���ֱ�������Σ�
���B=��C=45.
���ı���DEFG�dz����Σ�
���DEF=��GFE=90��.
�ߡ�DEF+��BED=180��.
���BED=90��.
��BE=DE=6.
��BE+CE=BC=16,
��CE= BC-BE=16-6=10.
�൱ˮƽ����d��10ʱ�������� DEFGǡ����ȫ�Ƴ����ǰ壻
(2)�ٵ�0<d��4ʱ����ͼ1��ʾ��
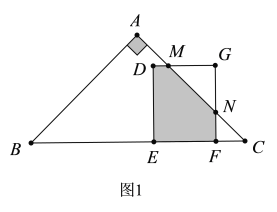
�ߡ�GNM=��FNC=��C=45������G=90����
��GN=GM=d.
��S=������DEFG�����-��GMN�����
=24-![]() ��
��
�ڵ�4<d��6ʱ����ͼ2��ʾ��
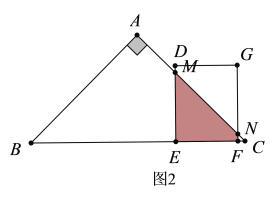
�������֪��BE=6+d,FC=6-d.
��BC=16,
��EC=16-BE=10-d.
�ߡ�C=45����
��ME= EC =10-d.FN= FC=6-d.
��S=��MEC���-��FCN�����
=![]()
=![]() ��10-d+6-d��(10-d-6+d)
��10-d+6-d��(10-d-6+d)
=32-4d.
�۵�6<d��10ʱ����ͼ2��ʾ��
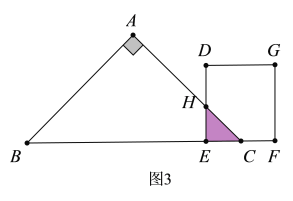
��EH=EC=10-d
��S=![]()
=![]()
�ܵ�10<dʱ,������DEFG����ABCû���ص����֣�
��S=0.
������������0<d��4ʱ��S=24-![]() ����4<d��6ʱ��S=32-4d����6<d��10ʱ��S=
����4<d��6ʱ��S=32-4d����6<d��10ʱ��S=![]() ����10<dʱ,S=0.
����10<dʱ,S=0.