ЬтФПФкШн
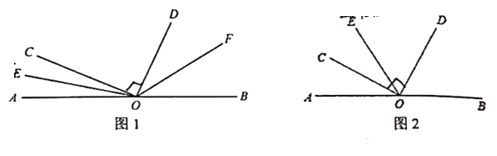
ЁОЬтФПЁПШчЭМЃЌСНЬѕжБЯпABЃЌCDЯрНЛгкЕуOЃЌЧвЁЯAOCЃНЁЯAODЃЌЩфЯпOMДгOBПЊЪМШЦOЕуФцЪБеыЗНЯђа§зЊЃЌЫйЖШЮЊ15Ёу/sЃЌЩфЯпONЭЌЪБДгODПЊЪМШЦOЕуЫГЪБеыЗНЯђа§зЊЃЌЫйЖШЮЊ12Ёу/sЃЌдЫЖЏЪБМфЮЊtУыЃЈ0ЃМtЃМ12ЃЌБОЬтГіЯжЕФНЧОљаЁгкЦННЧЃЉ
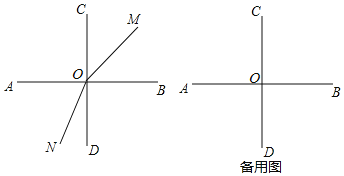
ЃЈ1ЃЉЭМжавЛЖЈгаЁЁ ЁЁИіжБНЧЃЛЕБtЃН2ЪБЃЌЁЯMONЕФЖШЪ§ЮЊЁЁ ЁЁЃЌЁЯBONЕФЖШЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєOEЦНЗжЁЯCOMЃЌOFЦНЗжЁЯNODЃЌЕБЁЯEOFЮЊжБНЧЪБЃЌЧыЧѓГіtЕФжЕЃЛ
ЃЈ3ЃЉЕБЩфЯпOMдкЁЯCOBФкВПЃЌЧв![]() ЪЧЖЈжЕЪБЃЌЧѓtЕФШЁжЕЗЖЮЇЃЌВЂЧѓГіетИіЖЈжЕЃЎ
ЪЧЖЈжЕЪБЃЌЧѓtЕФШЁжЕЗЖЮЇЃЌВЂЧѓГіетИіЖЈжЕЃЎ
ЁОД№АИЁП(1)4ЃЛ144ЁуЃЌ114ЁуЃЛ(2)tЕФжЕЮЊ10sЃЛ(3)ЕБЩфЯпOMдкЁЯCOBФкВПЃЌЧв![]() ЪЧЖЈжЕЪБЃЌtЕФШЁжЕЗЖЮЇЮЊ
ЪЧЖЈжЕЪБЃЌtЕФШЁжЕЗЖЮЇЮЊ![]() ЃМtЃМ6ЃЌетИіЖЈжЕЪЧ3
ЃМtЃМ6ЃЌетИіЖЈжЕЪЧ3
ЁОНтЮіЁП
(1)гЩжБЯпABЃЌCDЯрНЛгкЕуOЃЌЁЯAOCЃНЁЯAODМДПЩЕУЕНЙВ4ИіжБНЧЃЛЕБtЃН2ЪБЧѓЕУЁЯBOMЃН30ЁуЃЌЁЯNONЃН24ЁуЃЌМДПЩЕУЕНЁЯMONЁЂЁЯBONЕФЖШЪ§ЃЛ
(2)гУtЗжБ№БэЪОГіЁЯBOMЃН15tЃЌЁЯNODЃН12tЃЌЁЯCOMЃН15tЉ90ЁуЃЌИљОнOEЦНЗжЁЯCOMЃЌOFЦНЗжЁЯNODЃЌЗжБ№ЧѓЕУЁЯCOEЁЂЁЯDOF,гЩЁЯEOFЮЊжБНЧМДЁЯCOE+ЁЯDOFЃН90ЁуЃЌСаГіЗНГЬНтД№МДПЩ.
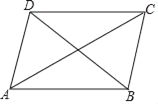
(3)ЯШШЗЖЈЁЯMONЃН180ЁуЪБЃЌЁЯBOMЃН90ЁуЪБtЕФжЕЃЌдйЗжСНжжЧщПіНјааМЦЫуЃЌЕУЕН0ЃМtЃМ![]() ЪБ
ЪБ![]() ВЛЪЧЖЈжЕЃЌЕБ
ВЛЪЧЖЈжЕЃЌЕБ![]() ЃМtЃМ6ЪБЃЌ
ЃМtЃМ6ЪБЃЌ![]() =3ЪЧЖЈжЕ.
=3ЪЧЖЈжЕ.
ЃЈ1ЃЉШчЭМЫљЪОЃЌЁпСНЬѕжБЯпABЃЌCDЯрНЛгкЕуOЃЌЁЯAOCЃНЁЯAODЃЌ
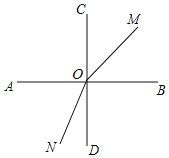
ЁрЁЯAOCЃНЁЯAODЃН90ЁуЃЌ
ЁрЁЯBOCЃНЁЯBODЃН90ЁуЃЌ
ЁрЭМжавЛЖЈга4ИіжБНЧЃЛ
ЕБtЃН2ЪБЃЌЁЯBOMЃН30ЁуЃЌЁЯNONЃН24ЁуЃЌ
ЁрЁЯMONЃН30Ёу+90Ёу+24ЁуЃН144ЁуЃЌ
ЁЯBONЃН90Ёу+24ЁуЃН114ЁуЃЛ
ЙЪД№АИЮЊЃК4ЃЛ144ЁуЃЌ114ЁуЃЛ
ЃЈ2ЃЉШчЭМЫљЪОЃЌЁЯBOMЃН15tЃЌЁЯNODЃН12tЃЌЁЯCOMЃН15tЉ90ЁуЃЌ
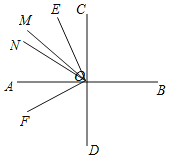
ЁпOEЦНЗжЁЯCOMЃЌOFЦНЗжЁЯNODЃЌ
ЁрЁЯCOEЃН![]() ЁЯCOMЃН
ЁЯCOMЃН![]() ЃЈ15tЉ90ЁуЃЉЃЌЁЯDOFЃН
ЃЈ15tЉ90ЁуЃЉЃЌЁЯDOFЃН![]() ЁЯDONЃН
ЁЯDONЃН![]() ЁС12tЃЌ
ЁС12tЃЌ
ЁпЕБЁЯEOFЮЊжБНЧЪБЃЌЁЯCOE+ЁЯDOFЃН90ЁуЃЌ
Ёр![]() ЃЈ15tЉ90ЁуЃЉЃН
ЃЈ15tЉ90ЁуЃЉЃН![]() ЁС12tЃЌ
ЁС12tЃЌ
НтЕУtЃН10ЃЌ
ЁрЕБЁЯEOFЮЊжБНЧЪБЃЌtЕФжЕЮЊ10sЃЛ
ЃЈ3ЃЉЕБЁЯMONЃН180ЁуЪБЃЌЁЯBOM+ЁЯBOD+ЁЯDONЃН180ЁуЃЌ
Ёр15t+90Ёу+12tЃН180ЁуЃЌ
НтЕУtЃН![]() ЃЌ
ЃЌ
ЕБЁЯBOMЃН90ЁуЪБЃЌ15tЃН90ЁуЃЌ
НтЕУtЃН6ЃЌ
ЂйШчЭМЫљЪОЃЌЕБ0ЃМtЃМ![]() ЪБЃЌ
ЪБЃЌ
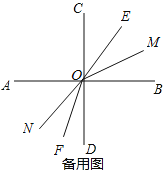
ЁЯCOMЃН90ЁуЉ15tЃЌЁЯBONЃН90Ёу+12tЃЌ
ЁЯMONЃНЁЯBOM+ЁЯBOD+ЁЯDONЃН15t+90Ёу+12tЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌЃЈВЛЪЧЖЈжЕЃЉ
ЃЌЃЈВЛЪЧЖЈжЕЃЉ
ЂкШчЭМЫљЪОЃЌЕБ![]() ЃМtЃМ6ЪБЃЌ
ЃМtЃМ6ЪБЃЌ
ЁЯCOMЃН90ЁуЉ15tЃЌЁЯBONЃН90Ёу+12tЃЌ
ЁЯMONЃН360ЁуЉЃЈЁЯBOM+ЁЯBOD+ЁЯDONЃЉЃН360ЁуЉЃЈ15t+90Ёу+12tЃЉЃН270ЁуЉ27tЃЌ
Ёр![]() ЃН
ЃН![]() =3ЃЌЃЈЪЧЖЈжЕЃЉ
=3ЃЌЃЈЪЧЖЈжЕЃЉ
злЩЯЫљЪіЃЌЕБЩфЯпOMдкЁЯCOBФкВПЃЌЧв![]() ЪЧЖЈжЕЪБЃЌtЕФШЁжЕЗЖЮЇЮЊ
ЪЧЖЈжЕЪБЃЌtЕФШЁжЕЗЖЮЇЮЊ![]() ЃМtЃМ6ЃЌетИіЖЈжЕЪЧ3ЃЎ
ЃМtЃМ6ЃЌетИіЖЈжЕЪЧ3ЃЎ

ЁОЬтФПЁПаЁЭѕЭЌбЇдкбЇаЃзщжЏЕФЩчЛсЕїВщЛюЖЏжаИКд№СЫНтЫћЫљОгзЁЕФаЁЧј450ЛЇОгУёЕФЩњЛюгУЫЎЧщПіЃЌЫћДгжаЫцЛњЕїВщСЫ50ЛЇОгУёЕФдТОљгУЫЎСПЃЈЕЅЮЛЃКtЃЉЃЌВЂЛцжЦСЫбљБОЕФЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃЈШчЭМЃЉЃЎ
дТОљгУЫЎСПЃЈЕЅЮЛЃКtЃЉ | ЦЕЪ§ | АйЗжБШ |
2ЁмxЃМ3 | 2 | 4% |
3ЁмxЃМ4 | 12 | 24% |
4ЁмxЃМ5 | ЁЁ ЁЁ | ЁЁ ЁЁ |
5ЁмxЃМ6 | 10 | 20% |
6ЁмxЃМ7 | ЁЁ ЁЁ | 12% |
7ЁмxЃМ8 | 3 | 6% |
8ЁмxЃМ9 | 2 | 4% |
ЃЈ1ЃЉЧыИљОнЬтжавбгаЕФаХЯЂВЙШЋЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ2ЃЉШчЙћМвЭЅдТОљгУЫЎСПЁАДѓгкЛђЕШгк4tЧваЁгк7tЁБЮЊжаЕШгУЫЎСПМвЭЅЃЌЧыФуЙРМЦзмЬхаЁЭѕЫљОгзЁЕФаЁЧјжаЕШгУЫЎСПМвЭЅДѓдМгаЖрЩйЛЇЃП
ЃЈ3ЃЉДгдТОљгУЫЎСПдк2ЁмxЃМ3ЃЌ8ЁмxЃМ9етСНИіЗЖЮЇФкЕФбљБОМвЭЅжаШЮвтГщШЁ2ИіЃЌЧыгУСаОйЗЈЃЈЛЪїзДЭМЛђСаБэЃЉЧѓГщШЁГіЕФ2ИіМвЭЅРДздВЛЭЌЗЖЮЇЕФИХТЪЃЎ

ЁОЬтФПЁПФГжабЇОйАьЁАаЃдАКУЩљвєЁБРЪЫаДѓШќЃЌИљОнГѕШќГЩМЈЃЌЦпФъМЖКЭАЫФъМЖИїбЁГі5УћбЁЪжзщГЩЦпФъМЖДњБэЖгКЭАЫФъМЖДњБэЖгВЮМгбЇаЃОіШќСНИіЖгИїбЁГіЕФ5УћбЁЪжЕФОіШќГЩМЈШчЭМЫљЪОЃК
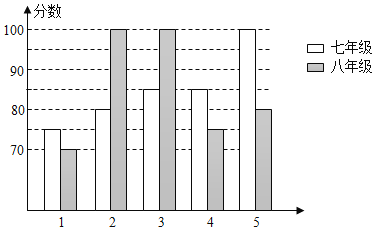
ЃЈ1ЃЉИљОнЫљИјаХЯЂЬюаДБэИёЃЛ
ЦНОљЪ§ЃЈЗжЃЉ | жаЮЛЪ§ЃЈЗжЃЉ | жкЪ§ЃЈЗжЃЉ | |
ЦпФъМЖ | 85 | ||
АЫФъМЖ | 85 | 100 |
ЃЈ2ЃЉНсКЯСНЖгГЩМЈЕФЦНОљЪ§КЭжаЮЛЪ§ЃЌЗжЮіФФИіЖгЕФОіШќГЩМЈНЯКУЃЛ
ЃЈ3ЃЉШєЦпФъМЖДњБэЖгОіШќГЩМЈЕФЗНВюЮЊ70ЃЌМЦЫуАЫФъМЖДњБэЖгОіШќГЩМЈЕФЗНВюЃЌВЂХаЖЯФФИіДњБэЖгЕФбЁЪжГЩМЈНЯЮЊЮШЖЈЃЎ