题目内容
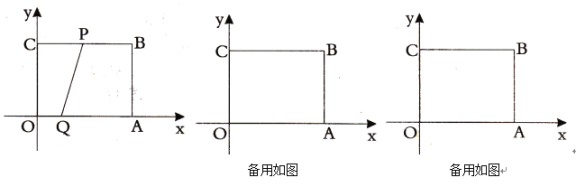
【题目】如图,矩形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,点
,点![]() 为
为![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠得到
折叠得到![]() ,且
,且![]() 落在线段
落在线段![]() 上,当
上,当![]() 时,则
时,则![]() 的长为___.
的长为___.
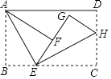
【答案】2
【解析】
由折叠可得∠AEH=![]() ∠BEC=90°,进而得出Rt△AEH中,AE2+EH2=AH2,设BE=x,则EF=x,CE=6-x=EG,再根据勾股定理,即可得到方程x2+42+(6-x)2+(6-2x)2=(2x-2)2+62,解该一元二次方程,即可得到BE的长.
∠BEC=90°,进而得出Rt△AEH中,AE2+EH2=AH2,设BE=x,则EF=x,CE=6-x=EG,再根据勾股定理,即可得到方程x2+42+(6-x)2+(6-2x)2=(2x-2)2+62,解该一元二次方程,即可得到BE的长.
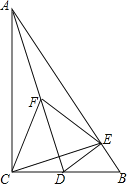
如图,连接AH,
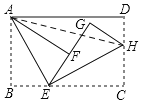
由折叠可得,BE=FE,EC=EG,GH=CH,∠AEB=∠AEF,∠CEH=∠GEH,
∴∠AEH=![]() ∠BEC=90°,
∠BEC=90°,
∴Rt△AEH中,AE2+EH2=AH2,①
设BE=x,则EF=x,CE=6-x=EG,
∴GF=6-2x=GH=CH,DH=4-(6-2x)=2x-2,
∵∠B=∠C=∠D=90°,
∴Rt△ABE中,AE2=EB2+AB2=x2+42,
Rt△CEH中,HE2=EC2+CH2=(6-x)2+(6-2x)2,
Rt△ADH中,AH2=DH2+AD2=(2x-2)2+62,
代入①式,可得
x2+42+(6-x)2+(6-2x)2=(2x-2)2+62,
解得x1=2,x2=12(舍去),
∴BE的长为2,
故答案为:2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目