题目内容
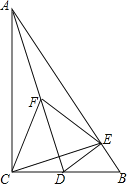
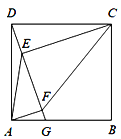
【题目】如图,在正方形ABCD中,点G在边AB上(不与点A,B重合),连接DG,作CE⊥DG于点E,AF⊥DG于点F,连接AE,CF.
(1)求证:DE=AF;
(2)若![]() 设
设![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1) 证![]() ,即可得DE=AF.
,即可得DE=AF.
(2)先证△AFG∽△CED,可得![]() ,根据正方形的性质等量代换得出
,根据正方形的性质等量代换得出![]() , 根据三角函数的定义求出tanα,tanβ的比例式,直接化简求解即可.
, 根据三角函数的定义求出tanα,tanβ的比例式,直接化简求解即可.
(1)∵四边形ABCD是正方形
∴AD=CD,∠ADC=90°
∵CE⊥DG,AF⊥DG
∴∠AFD=∠DEC=90°
∴∠ADF+∠CDE=90°,∠DCE+∠DEC=90°
∴∠ADF=∠DCE
在![]() 中,
中,
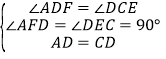
∴![]() (AAS)
(AAS)
∴DE=AF
(2)正方形ABCD中,AB∥CD,
∴∠AGF=∠CDE.
∵∠CED=∠AFG=90°,
∴△AFG∽△CED.
∴![]() .
.
∵![]() ,又AB=CD,∴
,又AB=CD,∴![]() .
.
∴![]() .
.
∴![]() .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目