Question

如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线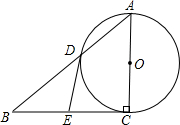，交BC于点E．
（1）求证：点E是边BC的中点；
（2）若EC=3，BD=2

6

，求⊙O的直径AC的长度；
（3）若以点O，D，E，C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由．

Answer 1

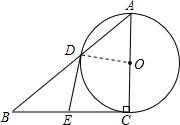
（1）证明：连接DO；
∵∠ACB=90°，AC为直径，
∴EC为⊙O的切线；
又∵ED也为⊙O的切线，
∴EC=ED，
又∵∠EDO=90°，
∴∠BDE+∠ADO=90°，
∴∠BDE+∠A=90°
又∵∠B+∠A=90°，
∴∠BDE=∠B，
∴EB=ED，
∴EB=EC，即点E是边BC的中点；

（2）∵BC，BA分别是⊙O的切线和割线，
∴BC²=BD•BA，
∴（2EC）²=BD•BA，即BA•2

6

=36，
∴BA=3

6

，
在Rt△ABC中，由勾股定理得
AC=

AB2-BC2

=

(3 6 )2-62

=3

2

；

（3）△ABC是等腰直角三角形．
理由：∵四边形ODEC为正方形，
∴∠DOC=∠ACB=90°，即DO∥BC，
又∵点E是边BC的中点，
∴BC=2OD=AC，
∴△ABC是等腰直角三角形．