题目内容
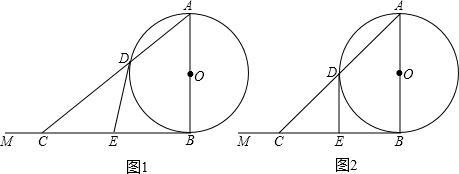
如图，△ABC内接于⊙O，过点B作⊙O的切线，交于CA的延长线于点E，∠EBC=2∠C．
（1）求证：AB=AC；
（2）当
=
时，①求tan∠ABE的值；②如果AE=
，求AC的值．
（1）求证：AB=AC；
（2）当
| AB |
| BC |
| ||
| 4 |
| 20 |
| 11 |
（1）证明：∵BE切⊙O于点B，
∴∠ABE=∠C．
∵∠EBC=2∠C，
即∠ABE+∠ABC=2∠C．
∴∠ABC=∠C．
∴AB=AC．
（2）①如图，连接AO，交BC于点F
∵AB=AC，∴
=
；
∴AO⊥BC，且BF=FC．
∵
=
∴
=
∴
=
；
设AB=
m，BF=2m，
由勾股定理，得AF=
=
=m；
∴tan∠ABE=tan∠ABF=
=
=
．
②在△EBA和△ECB中，
∵∠E=∠E，∠EBA=∠ECB，∴△EBA∽△ECB，
∴
=
；
∵
=
，
∴EB=
EA（※）；
由切割线定理，得EB2=EA×EC=EA（EA+AC）；
将（※）式代入上式，得
EA2=EA（EA+AC）；
∵EA≠0，
∴AC=
EA=
×
=4．
∴∠ABE=∠C．
∵∠EBC=2∠C，
即∠ABE+∠ABC=2∠C．
∴∠ABC=∠C．
∴AB=AC．
（2）①如图，连接AO，交BC于点F
∵AB=AC，∴
 |
| AB |
|
| AC |
∴AO⊥BC，且BF=FC．
∵
| AB |
| BC |
| ||
| 4 |
| AB |
| 2BF |
| ||
| 4 |
| AB |
| BF |
| ||
| 2 |
设AB=
| 5 |
由勾股定理，得AF=
| AB2-BF2 |
| 5m2-4m2 |
∴tan∠ABE=tan∠ABF=
| AF |
| BF |
| m |
| 2m |
| 1 |
| 2 |
②在△EBA和△ECB中，
∵∠E=∠E，∠EBA=∠ECB，∴△EBA∽△ECB，
∴
| EA |
| EB |
| AB |
| BC |
∵
| AB |
| BC |
| ||
| 4 |
∴EB=
| 4 | ||
|
由切割线定理，得EB2=EA×EC=EA（EA+AC）；
将（※）式代入上式，得
| 16 |
| 5 |
∵EA≠0，
∴AC=
| 11 |
| 5 |
| 11 |
| 5 |
| 20 |
| 11 |
练习册系列答案
全能测控期末小状元系列答案
相关题目
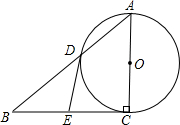，交BC于点E．
延长线于点D．
