题目内容
【题目】如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm? (结果精确到0.1cm,参考数据: ![]() ≈1.732)
≈1.732)
【答案】解:由题意得:AD⊥CE,过点B作BM⊥CE,BF⊥EA, ∵灯罩BC长为30cm,光线最佳时灯罩BC与水平线所成的角为30°,
∵CM⊥MB,即三角形CMB为直角三角形,
∴sin30°= ![]() =
= ![]() ,
,
∴CM=15cm,
在直角三角形ABF中,sin60°= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得:BF=20 ![]() ,
,
又∠ADC=∠BMD=∠BFD=90°,
∴四边形BFDM为矩形,
∴MD=BF,
∴CE=CM+MD+DE=CM+BF+ED=15+20 ![]() +2≈51.6cm.
+2≈51.6cm.
答:此时灯罩顶端C到桌面的高度CE是51.6cm.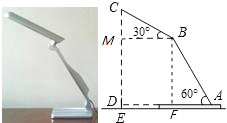
【解析】根据sin30°= ![]() ,求出CM的长,根据sin60°=
,求出CM的长,根据sin60°= ![]() ,求出BF的长,得出CE的长,即可得出CE的长.
,求出BF的长,得出CE的长,即可得出CE的长.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目