题目内容
【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F. 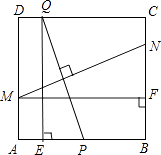
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴∠A=∠B=∠D=90°,AD=AB,
∵QE⊥AB,MF⊥BC,
∴∠AEQ=∠MFB=90°,
∴四边形ABFM、AEQD都是矩形,
∴MF=AB,QE=AD,MF⊥QE,
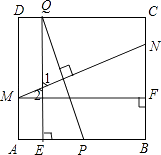
又∵PQ⊥MN,
∴∠1+∠EQP=90°,∠2+∠FMN=90°,
∵∠1=∠2,
∴∠EQP=∠FMN,
又∵∠QEP=∠MFN=90°,
∴△PEQ≌△NFM
(2)解:分为两种情况:①当E在AP上时,
∵点P是边AB的中点,AB=2,DQ=AE=t,
∴PA=1,PE=1﹣t,QE=2,
由勾股定理,得PQ= ![]() =
= ![]() ,
,
∵△PEQ≌△NFM,
∴MN=PQ= ![]() ,
,
又∵PQ⊥MN,
∴S= ![]() =
= ![]() =
= ![]() t2﹣t+
t2﹣t+ ![]() ,
,
∵0≤t≤2,
∴当t=1时,S最小值=2.
②当E在BP上时,
∵点P是边AB的中点,AB=2,DQ=AE=t,
∴PA=1,PE=t﹣1,QE=2,
由勾股定理,得PQ= ![]() =
= ![]() ,
,
∵△PEQ≌△NFM,
∴MN=PQ= ![]() ,
,
又∵PQ⊥MN,
∴S= ![]() =
= ![]() [(t﹣1)2+4]=
[(t﹣1)2+4]= ![]() t2﹣t+
t2﹣t+ ![]() ,
,
∵0≤t≤2,
∴当t=1时,S最小值=2.
综上:S= ![]() t2﹣t+
t2﹣t+ ![]() ,S的最小值为2.
,S的最小值为2.
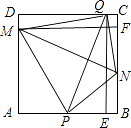
【解析】(1)由四边形ABCD是正方形得到∠A=∠B=∠D=90°,AD=AB,又由∠EQP=∠FMN,而证得;(2)分为两种情况:①当E在AP上时,由点P是边AB的中点,AB=2,DQ=AE=t,又由勾股定理求得PQ,由△PEQ≌△NFM得到PQ的值,又PQ⊥MN求得面积S,由t范围得到S的最小值;②当E在BP上时,同法可求S的最小值.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案