题目内容
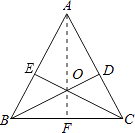
【题目】已知:如图,锐角△ABC的两条高BD、CE相交于点O,且OB=OC. 
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由.
【答案】
(1)证明:∵OB=OC,
∴∠OBC=∠OCB,
∵锐角△ABC的两条高BD、CE相交于点O,
∴∠BEC=∠CDB=90°,
∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°,
∴180°﹣∠BEC﹣∠BCE=180°﹣∠CDB﹣∠CBD,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形
(2)解:点O在∠BAC的角平分线上.
理由:连接AO并延长交BC于F,
在△AOB和△AOC中,
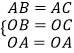
∴△AOB≌△AOC(SSS).
∴∠BAF=∠CAF,
∴点O在∠BAC的角平分线上.
【解析】(1)由OB=OC,即可求得∠OBC=∠OCB,又由,锐角△ABC的两条高BD、CE相交于点O,根据三角形的内角和等于180°,即可证得△ABC是等腰三角形;(2)首先连接AO并延长交BC于F,通过证△AOB≌△AOC(SSS),得到∠BAF=∠CAF,即点O在∠BAC的角平分线上.
【考点精析】关于本题考查的角平分线的性质定理和等腰三角形的判定,需要了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案【题目】某社区青年志愿者小分队年龄情况如下表所示:
年龄(岁) | 18 | 19 | 20 | 21 | 22 |
人数 | 2 | 5 | 2 | 2 | 1 |
则这12名队员年龄的众数、中位数分别是( )
A.2,20岁
B.2,19岁
C.19岁,20岁
D.19岁,19岁