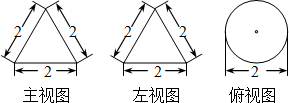
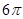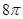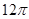题目内容
在△ABC中,AB=
,AC=
,BC=1.
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
| 3 |
| 2 |
(1)求证:∠A≠30°;
(2)将△ABC绕BC所在直线旋转一周,求所得几何体的表面积.
证明:(1)∵BC2+AC2=1+2=3=AB2,
∴△ABC是直角三角形,且∠C=90°.
∵sinA=
=
>
=sin30°,
∴∠A≠30°.
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,
∴圆锥的底面圆的半径=
,
∴圆锥的底面圆的周长=2π•
=2
π;母线长为
,
∴几何体的表面积
×
π+π×(
)2=
π+2π.

∴△ABC是直角三角形,且∠C=90°.
∵sinA=
| BC |
| AB |
| 1 | ||
|
| 1 |
| 2 |
∴∠A≠30°.
(2)将△ABC绕BC所在直线旋转一周,所得的几何体为圆锥,
∴圆锥的底面圆的半径=
| 2 |
∴圆锥的底面圆的周长=2π•
| 2 |
| 2 |
| 3 |
∴几何体的表面积
| 2 |
| 3 |
| 2 |
| 6 |


练习册系列答案
相关题目