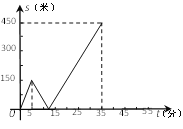
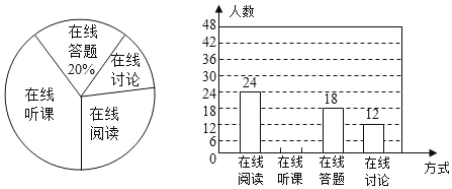
题目内容
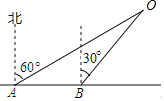
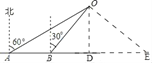
【题目】如图,某轮船在海上向正东方向航行,上午8:00在点A处测得小岛O在北偏东60°方向的16![]() km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
km处;上午8:30轮船到达B处,测得小岛O在北偏东30°方向.
(1)求轮船从A处到B处的航速;
(2)如果轮船按原速继续向东航行,还需经过多少时间轮船才恰好位于小岛的东南方向?
【答案】(1) 32(km/h);(2)![]() .
.
【解析】
(1)过点O作OD⊥AB,垂足为D,根据三角函数的应用即可求出AB,进而求出速度;(2)过点O作∠DOE=45°交AD的延长线与点E,先求出DE,再得出BE,则求出时间.
解:(1)如图,过点O作OD⊥AB,垂足为D.
有题意知:∠OAD=30°,∠OBD=60°.
在Rt△OAD中,∵OA=16![]() ,∠OAD=30°,
,∠OAD=30°,
∴OD=8![]() ,AD=24.
,AD=24.
在Rt△OBD中,∵OD=8![]() ,∠OBD=60°.
,∠OBD=60°.
∴BD=![]() =
=![]() =8,
=8,
∴AB=AD﹣BD=24﹣8=16(km),
∴v=![]() =32(km/h)
=32(km/h)
答:轮船从A处到B处的航速为32km/h.
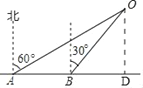
(2)过点O作∠DOE=45°交AD的延长线与点E.
∵∠DOE=45°,∠ODE=90°,
∴DE=OD=8![]() km,
km,
BE=BD+DE=8+8![]() (km),
(km),
∵![]() =
=![]() (h),
(h),
答:轮船按原速继续向东航行,还需要航行![]() 小时才恰好位于小岛的东南方向.
小时才恰好位于小岛的东南方向.

 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】小涛根据学习函数的经验,对函数![]() 的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
的图像与性质进行了探究,下面是小涛的探究过程,请补充完整:
(1)下表是![]() 与
与![]() 的几组对应值
的几组对应值
| ... | -2 | -1 | 0 | 1 | 2 |
| 3 | ... |
| ... | -8 | -3 | 0 | m | n | 1 | 3 | ... |
请直接写出:![]() =, m=, n=;
=, m=, n=;
(2)如图,小涛在平面直角坐标系中,描出了上表中已经给出的部分对应值为坐标的点,再描出剩下的点,并画出该函数的图象;
(3)请直接写出函数![]() 的图像性质:;(写出一条即可)
的图像性质:;(写出一条即可)
(4)请结合画出的函数图象,解决问题:若方程![]() 有三个不同的解,直接写出
有三个不同的解,直接写出![]() 的取值范围.
的取值范围.