题目内容
【题目】抛物线y=
x2-mx+m2-2（m为大于0的常数）与x轴交于A，B两点（点A在点B的左侧）
（1）若点A的坐标为（1，0）
①求抛物线的表达式；
②当n≤x≤2时，函数值y的取值范围是-
≤y≤5-n，求n的值；
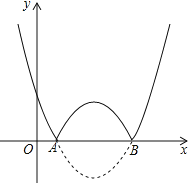
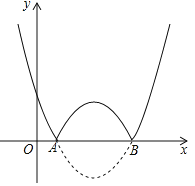
（2）将抛物线在x轴下方的部分沿x轴翻折，得到新的函数的图象，如图，当2＜x＜3时，若此函数的值随x的增大而减小，直接写出m的取值范围．
【答案】（1）①y=
x2-3x+
n的值为-1；（2）1≤m≤2或m≥5．
【解析】
（1）①将点A（1，0）代入y=x2-mx+m2-2，可求m,再求解析式；②根据所求二次函数解析式，从函数图像的变化情况得n2-3n+
=5-n，解方程可得n;（2）由y=0时，x2-mx+m2-2=0，可求出点A,B的坐标，抛物线的对称轴x=-
=m；①当m＞3时，有m-2≥3；②当m≤2时，有m+2≥3，综上所述：可得m的取值范围．
解：（1）①将点A（1，0）代入y=x2-mx+m2-2，得：0=-m+m2-2，
解得：m1=3，m2=-1（舍去），
∴抛物线的表达式为y=x2-3x+．
②∵抛物线的表达式为y=x2-3x+，
∴抛物线开口向上，对称轴为直线x=-
=3，
∴当n≤x≤2时，y随x的增大而减小．
∵当n≤x≤2时，函数值y的取值范围是-
≤y≤5-n，
∴n2-3n+=5-n，即n2-4n-5=0，
解得：n1=5（不合题意，舍去），n2=-1，
∴n的值为-1．
（2）当y=0时，x2-mx+m2-2=0，即[x-（m+2）][x-（m-2）]=0，
解得：x1=m-2，x2=m+2，
∴点A的坐标为（m-2，0），点B的坐标为（m+2，0）．
∵抛物线的表达式为y=x2-mx+m2-2，
∴对称轴为直线x=-=m．
①当m＞3时，有m-2≥3，
解得：m≥5；
②当m≤2时，有m+2≥3，
解得：m≥1，
∴1≤m≤2．
综上所述：m的取值范围为1≤m≤2或m≥5．
