题目内容
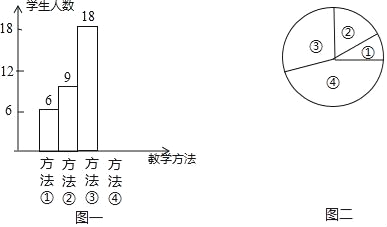
【题目】如图,△ABC中,∠A=60°,BM⊥AC于点M,CN⊥AB于点N,BM,CN交于点O,连接MN.下列结论:①∠AMN=∠ABC;②图中共有8对相似三角形;③BC=2MN.其中正确的个数是( )
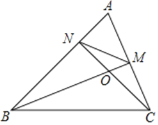
A. 1个B. 2个C. 3个D. 0个
【答案】C
【解析】
根据两角对应相等得出△ABM∽△ACN,即可得出△AMN∽△ABC,进而得到∠AMN=∠ABC;依据△ABM∽△ACN∽△OBN∽△OCM,△AMN∽△ABC,△BCO∽△NMO,可得图中共有8对相似三角形;依据AN=![]() AC,△AMN∽△ABC,即可得到
AC,△AMN∽△ABC,即可得到![]() ,即BC=2MN.
,即BC=2MN.
解:∵BM⊥AC,CN⊥AB,
∴∠ANC=∠AMB=90°,
又∵∠A=∠A,
∴△ABM∽△ACN,
∴![]() ,即
,即![]() ,
,
又∵∠A=∠A,
∴△AMN∽△ABC,
∴∠AMN=∠ABC,故①正确;
根据两角对应相等得出:△ABM∽△ACN∽△OBN∽△OCM,
△AMN∽△ABC,△BCO∽△NMO,
∴图中共有8对相似三角形,故②正确;
∵Rt△ACN中,∠A=60°,
∴∠ACN=30°,
∴AN=![]() AC,
AC,
又∵△AMN∽△ABC,
∴![]() ,
,
即BC=2MN,故③正确.
故选:C.

练习册系列答案
相关题目