题目内容
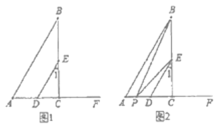
【题目】如图1,![]() 于点
于点![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)如图2,点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 运动到点
运动到点![]() 停止,连接
停止,连接![]() 、
、![]() .则
.则![]() 、
、![]() 、
、![]() 三个角之间具有怎样的数量关系(不考虑点
三个角之间具有怎样的数量关系(不考虑点![]() 与点
与点![]() ,
,![]() ,
,![]() 重合的情况)?并说明理由.
重合的情况)?并说明理由.
【答案】(1)见详解;(2)当点P在A,D之间时,![]() ;当点P在C,D之间时,
;当点P在C,D之间时,![]() ;当点P在C,F之间时,
;当点P在C,F之间时,![]() .
.
【解析】
(1)根据∠A+∠B=90°,∠A+∠1=90°,即可得到∠B=∠1,进而得出AB∥DE.
(2)分三种情况讨论:点P在A,D之间;点P在C,D之间;点P在C,F之间;分别过P作PG∥AB,利用平行线的性质,即可得到∠ABP,∠DEP,∠BPE三个角之间的数量关系.
解:(1)如图1,∵BC⊥AF于点C,
∴∠A+∠B=90°,
又∵∠A+∠1=90°,
∴∠B=∠1,
∴AB∥DE.
(2)如图2,当点P在A,D之间时,过P作PG∥AB,

∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG+∠EPG=∠ABP+∠DEP;
∴![]() ;
;
如图所示,当点P在C,D之间时,过P作PG∥AB,
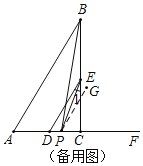
∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠BPG-∠EPG=∠ABP-∠DEP;
∴![]() ;
;
如图所示,当点P在C,F之间时,过P作PG∥AB,

∵AB∥DE,
∴PG∥DE,
∴∠ABP=∠GPB,∠DEP=∠GPE,
∴∠BPE=∠EPG-∠BPG=∠DEP-∠ABP.
∴![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目