题目内容
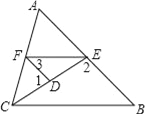
【题目】在一次数学探究活动中:如图,在△ABC中,AB=5,AC=9,AD是BC边上的中线,
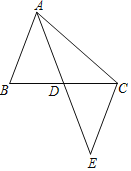
求AD的取值范围.小明给出了一种方法,步骤如下:
①过点C作一条与AB平行的线;
②延长AD交这条平行线于点E;
③通过证明得到AD=DE,AB=CE;
④利用△ACE三边的数量关系得到AD的取值范围.
根据这个方法,请你完成下面两个问题:
(1)求证:AD=DE,AB=CE;
(2)求AD的取值范围.
【答案】(1)见解析;(2)2<AD<7.
【解析】
(1)证明△ADB≌△EDC(ASA)即可解决问题.
(2)利用全等三角形的性质以及三角形的三边关系解决问题即可.
(1)证明:∵AB∥CD,
∴∠B=∠DCE,
在△ADB和△EDC中,
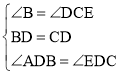 ,
,
∴△ADB≌△EDC(ASA),
∴AD=DE,AB=CE.
(2)解:∵AC=9,EC=AB=5,
∴9﹣5<AE<5+9,
∴4<AE<14,
∵AD=DE,
∴AE=2AD,
∴4<2AD<14,
∴2<AD<7.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目