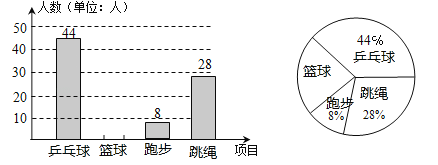
题目内容
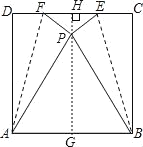
【题目】如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE,如果正方形ABCD的边长是2,那么△EPF的面积是_____.

【答案】![]()
【解析】
过P作PH⊥DC于H,交AB于G,由正方形的性质得到AD=AB=BC=DC=2;∠D=∠C=90°;再根据折叠的性质有PA=PB=2,∠FPA=∠EPB=90°,可判断△PAB为等边三角形,利用等边三角形的性质得到∠APB=60°,![]() ,于是∠EPF=120°,PH=HG﹣PG=2﹣
,于是∠EPF=120°,PH=HG﹣PG=2﹣![]() ,得∠HEP=30°,然后根据含30°的直角三角形三边可求出HE,得到EF,最后利用三角形的面积公式计算即可.
,得∠HEP=30°,然后根据含30°的直角三角形三边可求出HE,得到EF,最后利用三角形的面积公式计算即可.
解:过P作PH⊥DC于H,交AB于G,如图,
则PG⊥AB,
∵四边形ABCD为正方形,
∴AD=AB=BC=DC=2;∠D=∠C=90°,
又∵将正方形ABCD折叠,使点C与点D重合于形内点P处,
∴PA=PB=2,∠FPA=∠EPB=90°,
∴△PAB为等边三角形,
∴∠APB=60°,PG=![]() AB=
AB=![]() ,
,
∴∠EPF=120°,PH=HG﹣PG=2﹣![]() ,
,
∴∠HEP=30°,
∴HE=![]() PH=
PH=![]() (2﹣
(2﹣![]() )=2
)=2![]() ﹣3,
﹣3,
∴EF=2HE=4![]() ﹣6,
﹣6,
∴△EPF的面积=![]() FEPH=
FEPH=![]() (2﹣
(2﹣![]() )(4
)(4![]() ﹣6)
﹣6)
=7![]() ﹣12.
﹣12.
故答案为7![]() ﹣12.
﹣12.

练习册系列答案
相关题目