��Ŀ����
����Ŀ��Ϊ����ף���й�����70���꣬ijУ��֯���꼶ȫ��ѧ���μӡ�ǡͬѧ���꣬��������¡����й�����70����֪ʶ��������������ȡ�IJ���ѧ���ɼ�����������ֳ�5�飬50��60�֣�![]() ����С���Ϊ��ѧͯ���飬60��70��(
����С���Ϊ��ѧͯ���飬60��70��(![]() )��С���Ϊ����š��飬70��80��(
)��С���Ϊ����š��飬70��80��(![]() )��С���Ϊ�����ˡ��飬80��90��(
)��С���Ϊ�����ˡ��飬80��90��(![]() )��С���Ϊ����ʿ���飬90��100��(
)��С���Ϊ����ʿ���飬90��100��(![]() )��С���Ϊ�����֡��飬�������˲�������Ƶ���ֲ�ֱ��ͼ���£������ṩ����Ϣ����������⣺
)��С���Ϊ�����֡��飬�������˲�������Ƶ���ֲ�ֱ��ͼ���£������ṩ����Ϣ����������⣺
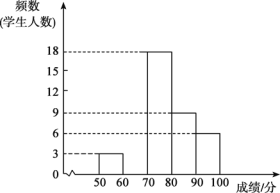
��1���������֡���ɼ���Ƶ����12.5�����벹ȫƵ���ֲ�ֱ��ͼ��
��2���ڴ˴α����У���ȡѧ���ijɼ�����λ���� �飻
��3��ѧУ�����Գɼ���70��100��(![]() )��ѧ�����н����������꼶����336��ѧ������ͨ������˵������Լ�ж�����ѧ����?
)��ѧ�����н����������꼶����336��ѧ������ͨ������˵������Լ�ж�����ѧ����?
���𰸡���1�������������2��70~80���ˡ�����3��231.
��������
��1���ȸ���90��100�ֵ�����������ռ�ٷֱ���������������ɸ�������֮�͵������������60��70�ֵ��������Ӷ���ȫͼ�Σ�
��2��������λ���Ķ������ɵã�
��3�������������������˼�����ɵã�
�⣺��1���߱������������Ϊ6��12.5%=48���ˣ���
��60��70�ֵ�����Ϊ48-��3+18+9+6��=12���ˣ���
��ȫƵ���ֲ�ֱ��ͼ���£�
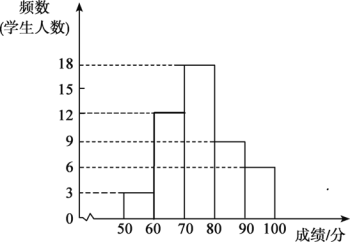
��2����Ϊ��λ���ǵ�24��25�����ݵ�ƽ����������24��25�����ݶ�����70��80����һ�飬
�����ڴ˴α����У���ȡѧ���ijɼ�����λ����70~80�����������飬
�ʴ�Ϊ��70~80������������
��3��![]() ��
��
�𣺴�Լ��231��ѧ����
�ʴ�Ϊ����1�������������2��70~80��������������3��231.