题目内容
【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,BC=10,对角线AC、BD相交于点O,且AC⊥BD,设AD=x,△AOB的面积为y.
(1)求∠DBC的度数;
(2)求y关于x的函数解析式,并写出自变量x的取值范围;
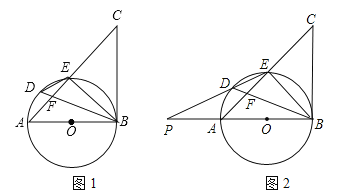
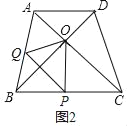
(3)如图1,设点P、Q分别是边BC、AB的中点,分别联结OP,OQ,PQ.如果△OPQ是等腰三角形,求AD的长.

【答案】(1)∠DBC=45;(2)y=![]() x(x>0);(3)满足条件的AD的值为10
x(x>0);(3)满足条件的AD的值为10![]() ﹣10.
﹣10.
【解析】
(1)过点D作AC的平行线DE,与BC的延长线交于E点,只要证明△BDE是等腰直角三角形即可解决问题;
(2)由(1)可知:△BOC,△AOD都是等腰直角三角形,由题意OA=![]() x,OB=5
x,OB=5![]() ,根据y=
,根据y=![]() OAOB计算即可;
OAOB计算即可;
(3)分三种情形讨论即可解决问题;
(1)过点D作AC的平行线DE,与BC的延长线交于E点.
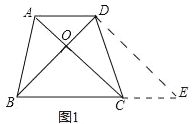
∵梯形ABCD中,AD∥BC,AC∥DE,
∴四边形ACED为平行四边形,AC=DE,AD=CE,
∵AB=CD,
∴梯形ABCD为等腰梯形,
∴AC=BD,
∴BD=DE,
又AC⊥BD,
∴∠BOC=90°
∵AC∥DE
∴∠BDE=90°,
∴△BDE是等腰直角三角形,
∴∠DBC=45°.
(2)由(1)可知:△BOC,△AOD都是等腰直角三角形,
∵AD=x,BC=10,
∴OA=![]() x,OB=5
x,OB=5![]() ,
,
∴y=![]() .
.
(3)如图2中,
①当PQ=PO=![]() BC=5时,
BC=5时,
∵AQ=QB,BP=PC=5,
∴PQ∥AC,PQ=![]() AC,
AC,
∴AC=10,∵OC=5![]() ,
,
∴OA=10﹣5![]() ,
,
∴AD=![]() OA=10
OA=10![]() ﹣10.
﹣10.
②当OQ=OP=5时,AB=2OQ=10,此时AB=BC,∠BAC=∠BCA=45°,
∴∠ABC=90°,同理可证:∠DCB=90°,
∴四边形ABCD是矩形,不符合题意,此种情形不存在.
③当OQ=PQ时,AB=2OQ,AC=2PQ,
∴AB=AC,
∴∠ABC=∠ACB=45°,
∴∠BAC=90°=∠BOC,显然不可能,
综上所述,满足条件的AD的值为10![]() ﹣10.
﹣10.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案