ЬтФПФкШн
ЁОЬтФПЁПИХФюШЯЪЖ
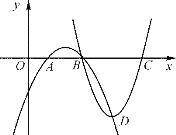
ЦНУцФкЃЌMЮЊЭМаЮTЩЯШЮвтвЛЕуЃЌNЮЊЁбOЩЯШЮвтвЛЕуЃЌНЋMЁЂNСНЕуМфОрРыЕФзюаЁжЕГЦЮЊЭМаЮTЕНЁбOЕФЁАзюНќОрРыЁБЃЌМЧзїdЃЈTЉЁбOЃЉЃЎР§ШчЭМЂйЃЌдкжБЯпlЩЯгаAЁЂBЁЂOШ§ЕуЃЌвдABЮЊвЛБпзїЕШБпЁїABCЃЌвдЕуOЮЊдВаФзїдВЃЌгыlНЛгкDЁЂEСНЕуЃЌШєНЋЁїABCМЧЮЊЭМаЮTЃЌдђBЁЂDСНЕуМфЕФОрРыГЦЮЊЭМаЮTЕНЁбOЕФЁАзюНќОрРыЁБЃЎ
Ъ§бЇРэНт
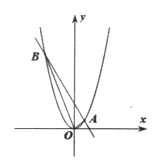
ЃЈ1ЃЉдкжБЯпlЩЯгаAЁЂBСНЕуЃЌвдЕуAЮЊдВаФЃЌ3ЮЊАыОЖзїЁбAЃЌНЋЕуBМЧЮЊЭМаЮTЃЌШєdЃЈTЉЁбAЃЉЃН1ЃЌдђABЃНЁЁ ЁЁЃЎ
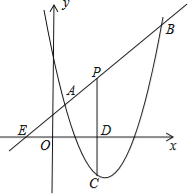
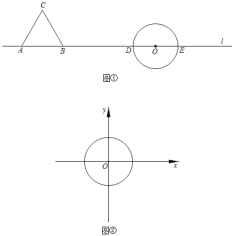
ЃЈ2ЃЉШчЭМЂкЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвдOЃЈ0ЃЌ0ЃЉЮЊдВаФЃЌАыОЖЮЊ2зїдВЃЎ
ЂйНЋЕуCЃЈ4ЃЌ3ЃЉМЧЮЊЭМаЮTЃЌдђdЃЈTЉЁбOЃЉЃНЁЁ ЁЁЃЎ
ЂкНЋвЛДЮКЏЪ§yЃНkx+2![]() ЕФЭММЧЮЊЭМаЮTЃЌШєdЃЈTЉЁбOЃЉЃО0ЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ЕФЭММЧЮЊЭМаЮTЃЌШєdЃЈTЉЁбOЃЉЃО0ЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ЭЦЙудЫгУ
ЃЈ3ЃЉдкЦНУцжБНЧзјБъЯЕжаЃЌPЕФзјБъЮЊЃЈtЃЌ0ЃЉЃЌЁбPЕФАыОЖЮЊ2ЃЌDЁЂEСНЕуЕФзјБъЗжБ№ЮЊЃЈЉ8ЃЌ8ЃЉЁЂЃЈЉ8ЃЌЉ8ЃЉЃЌНЋЁЯDOEМЧЮЊЭМаЮTЃЌШєdЃЈTЉЁбPЃЉЃН1ЃЌдђtЃНЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2Лђ4ЃЛЃЈ2ЃЉЂй3ЃЛЂкЉ1ЃМkЃМ1ЧвkЁй0ЃЛЃЈ3ЃЉЉ3![]() Лђ3ЃЎ
Лђ3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнdЃЈTЉЁбAЃЉЃН1ПЩЕУCBЃНCBЁфЃН1ЃЌгЩACЃН3МДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉЂйСЌНгOCВЂЧѓГіOCЕФГЄЖШМДПЩЕУГіД№АИЃЛ
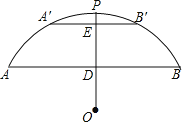
ЂкЩшжБЯпyЃНkx+![]() гыyжсЕФНЛЕуЮЊDЃЌгыЁбOЯрЧагкEЃЌKЃЌСЌНгOKЃЌOEЃЌЧѓГіDKЁЂDEЕФГЄЖШжЄУїЫФБпаЮDEOKЪЧе§ЗНаЮЃЌЕУЕНЁЯODEЃНЁЯODKЃН45ЁуЃЌШЛКѓИљОнdЃЈTЉЁбOЃЉЃО0МДПЩЕУГіД№АИЃЛ
гыyжсЕФНЛЕуЮЊDЃЌгыЁбOЯрЧагкEЃЌKЃЌСЌНгOKЃЌOEЃЌЧѓГіDKЁЂDEЕФГЄЖШжЄУїЫФБпаЮDEOKЪЧе§ЗНаЮЃЌЕУЕНЁЯODEЃНЁЯODKЃН45ЁуЃЌШЛКѓИљОнdЃЈTЉЁбOЃЉЃО0МДПЩЕУГіД№АИЃЛ
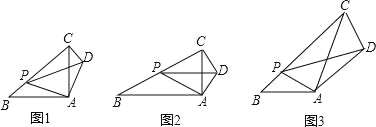
ЃЈ3ЃЉЗжСНжжЧщаЮЃКЂйШчЭМ31жаЃЌЕБЕуPдкЁЯDOEФкВПЪБЃЌзїPMЁЭODгкMЃЌНЛЁбPгкKЃЎЂкШчЭМ32жаЃЌЕБЕуPдкЁЯDOEЕФЭтВрЪБЃЌЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌ
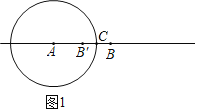
ЁпdЃЈTЉЁбAЃЉЃН1ЃЌ
ЁрCBЃНCBЁфЃН1ЃЌ
ЁпACЃН3ЃЌ
ЁрABЁфЃН2ЃЌABЃН4ЃЎ
ЙЪД№АИЮЊ2Лђ4ЃЎ
ЃЈ2ЃЉЂйШчЭМ2жаЃЌСЌНгOCНЛЁбOгкEЃЎ
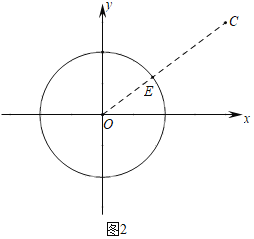
ЁпCЃЈ4ЃЌ3ЃЉЃЌ
ЁрOCЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁпOEЃН2ЃЌ
ЁрECЃН3ЃЌ
ЁрdЃЈTЉЁбOЃЉЃН3ЃЎ
ЙЪД№АИЮЊ3ЃЎ
ЂкШчЭМЃЌЩшжБЯпyЃНkx+![]() гыyжсЕФНЛЕуЮЊDЃЌгыЁбOЯрЧагкEЃЌKЃЎСЌНгOKЃЌOEЃЎ
гыyжсЕФНЛЕуЮЊDЃЌгыЁбOЯрЧагкEЃЌKЃЎСЌНгOKЃЌOEЃЎ
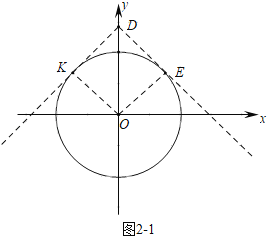
ЁпOEЁЭDEЃЌOKЁЭDKЃЌODЃН![]() ЃЌOEЃНOKЃН2ЃЌ
ЃЌOEЃНOKЃН2ЃЌ
ЁрDKЃН![]() ЃН2ЃЌDEЃН
ЃН2ЃЌDEЃН![]() ЃН2ЃЌ
ЃН2ЃЌ
ЁрDEЃНOEЃНDKЃНOKЃЌ
ЁрЫФБпаЮDEOKЪЧСтаЮЃЌ
ЁпЁЯDKOЃНЁЯDEOЃН90ЁуЃЌ
ЁрЫФБпаЮDEOKЪЧе§ЗНаЮЃЌ
ЁрЁЯODEЃНЁЯODKЃН45ЁуЃЌ
ЁржБЯпDEЕФНтЮіЪНЮЊyЃНЉx+![]() ЃЌжБЯпDKЕФНтЮіЪНЮЊyЃНx+
ЃЌжБЯпDKЕФНтЮіЪНЮЊyЃНx+![]() ЃЌ
ЃЌ
ЁпdЃЈTЉЁбOЃЉ0ЃЌ
ЁрЙлВьЭМЯѓПЩжЊТњзуЬѕМўЕФkЕФжЕЮЊЉ1ЃМkЃМ1ЧвkЁй0ЃЎ
ЃЈ3ЃЉШчЭМ3Љ1жаЃЌЕБЕуPдкЁЯDOEФкВПЪБЃЌзїPMЁЭODгкMЃЌНЛЁбPгкKЃЎ
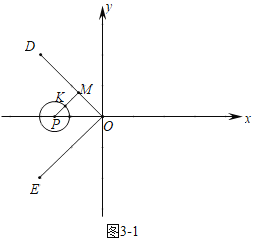
ЁпDЃЈЉ8ЃЌ8ЃЉЃЌ
ЁрЁЯDOPЃН45ЁуЃЌ
ЁпdЃЈTЉЁбPЃЉЃН1ЃЌ
ЁрPMЃНOMЃН3ЃЌOPЃН![]() ЃЌ
ЃЌ
ЁрtЃНЉ![]() ЃЎ
ЃЎ
ШчЭМ3Љ2жаЃЌЕБЕуPдкЁЯDOEЕФЭтВрЪБЃЌгЩЬтвтПЩжЊOMЃН1ЃЌOPЃН1+2ЃН3ЃЌtЃН3ЃЎ
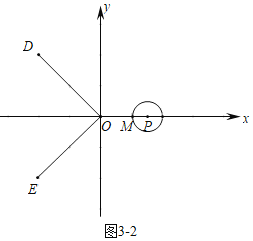
злЩЯЫљЪіЃЌТњзуЬѕМўЕФtЕФжЕЮЊЉ![]() Лђ3ЃЎ
Лђ3ЃЎ