��Ŀ����
����Ŀ����ͼ����ͬһƽ��ֱ������ϵ�У����κ���y��ax2��bx��c����κ���y��(a��3)x2��(b��15)x��c��18��ͼ����x��Ľ���ֱ���A��B��C��
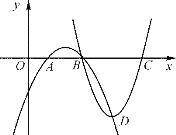
(1)�ж�ͼ�о�����B��D��C��ͼ������һ�����κ�����ͼ����˵�����ɣ�
(2)������������ͼ������B��D�����B��D�ĺ����꣮
(3)����D�ǹ���B��D��C�ĺ���ͼ��Ķ��㣬������Ϊ��2���������������Ľ���ʽ��
���𰸡���1��y��(a��3) x2��(b��15)x��c��18����2��2��3����3��y����x2 ��3x��2
��������
��1���������⣬���������ߣ�һ���������£�һ���������ϣ���Ƚ϶�����ϵ�����ɵõ��𰸣�
��2�����������������ʽ����ɷ����飬���x��ֵ�����ɵõ���B��D�ĺ����ꣻ
��3���������⣬�õ�����D�����꣬Ȼ��ѵ�B��2��0�����룬���ɵõ�����ʽ.
�⣺��1���������⣬�������߿��ڣ�һ���������£�һ���������ϣ�
��a��3>a��
�ྭ��B��D��C��ͼ���ǣ�y��(a��3) x2��(b��15)x��c��18��ͼ��
��2���ⷽ����
�����ã�![]() ��
��
��ã�x1��2��x2��3��
���B��D�ĺ�����ֱ�Ϊ2��3��
��3�������֪����D����Ϊ��3����2����
���������ʽΪ��y�� a (x��3)2��2��
�ѵ�B������(2��0)���룬��
![]() ��
��
��ã�a��2��
��![]() ��
��
��y��2x2��12x��16��
��![]() ��
��
��![]() ��
��
����������ߵĽ���ʽΪ��y����x2 ��3x��2��

 ��У����ϵ�д�
��У����ϵ�д�