题目内容
在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AB=8,BC=14,点E、F分别在边AB、CD上,EF∥AD ,点P与AD在直线EF的两侧,∠EPF=90°,PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.
,点P与AD在直线EF的两侧,∠EPF=90°,PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.
(1)求边AD的长;
(2)如图,当点P在梯形ABCD内部时,求y关于x的函数解析式,并写出定义域;
(3)如果MN的长为2,求梯形AEFD的面积.
 ,点P与AD在直线EF的两侧,∠EPF=90°,PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.
,点P与AD在直线EF的两侧,∠EPF=90°,PE=PF,射线EP、FP与边BC分别相交于点M、N,设AE=x,MN=y.(1)求边AD的长;
(2)如图,当点P在梯形ABCD内部时,求y关于x的函数解析式,并写出定义域;
(3)如果MN的长为2,求梯形AEFD的面积.
(1)过D作DH⊥BC,DH与EF、BC分别相交于点G、H,
∵梯形ABCD中,∠B=90°,
∴DH∥AB,
又∵AD∥BC,
∴四边形ABHD是矩形,
∵∠C=45°,
∴∠CDH=45°,
∴CH=DH=AB=8,
∴AD=BH=BC-CH=6.
(2)∵DH⊥EF,∠DFE=∠C=∠FDG=45°,
∴FG=DG=AE=x,
∵EG=AD=6,
∴EF=x+6,
∵PE=PF,EF∥BC,
∴∠PFE=∠PEF=∠PMN=∠PNM,
∴PM=PN,
过点P作QR⊥EF,QR与EF、MN分别相交于Q、R,
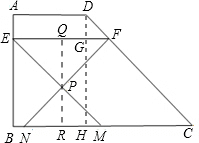 ∵∠MPN=∠EPF=90°,QR⊥MN,
∵∠MPN=∠EPF=90°,QR⊥MN,
∴PQ=
EF=
(x+6),PR=
MN=
y,
∵QR=BE=8-x,
∴
(x+6)+
y=8-x,
∴y关于x的函数解析式为y=-3x+10.定义域为1≤x<
.
(3)当点P在梯形ABCD内部时,由MN=2及(2)的结论得2=-3x+10,AE=x=
,
∴S梯形AEFD=
(AD+EF)•AE=
(6+6+
)×
=
,
当点P在梯形ABCD外部时,由MN=2及与(2)相同的方法得:
(x+6)-
×2=8-x,AE=x=4,
∴S梯形AEFD=
(AD+EF)•AE=
(6+6+4)×4=32.
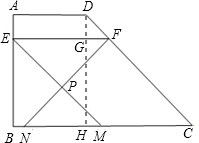
∵梯形ABCD中,∠B=90°,
∴DH∥AB,
又∵AD∥BC,
∴四边形ABHD是矩形,
∵∠C=45°,
∴∠CDH=45°,
∴CH=DH=AB=8,
∴AD=BH=BC-CH=6.
(2)∵DH⊥EF,∠DFE=∠C=∠FDG=45°,
∴FG=DG=AE=x,
∵EG=AD=6,
∴EF=x+6,
∵PE=PF,EF∥BC,
∴∠PFE=∠PEF=∠PMN=∠PNM,
∴PM=PN,
过点P作QR⊥EF,QR与EF、MN分别相交于Q、R,
 ∵∠MPN=∠EPF=90°,QR⊥MN,
∵∠MPN=∠EPF=90°,QR⊥MN,∴PQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵QR=BE=8-x,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴y关于x的函数解析式为y=-3x+10.定义域为1≤x<
| 10 |
| 3 |
(3)当点P在梯形ABCD内部时,由MN=2及(2)的结论得2=-3x+10,AE=x=
| 8 |
| 3 |
∴S梯形AEFD=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
| 176 |
| 9 |
当点P在梯形ABCD外部时,由MN=2及与(2)相同的方法得:
| 1 |
| 2 |
| 1 |
| 2 |
∴S梯形AEFD=
| 1 |
| 2 |
| 1 |
| 2 |


练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目




