题目内容
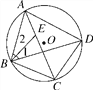
【题目】如图,AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D.P为AB延长线上一点,∠PCD=2∠BAC.
(1)求证:CP为⊙O的切线;
(2)若BP=1,CP=![]() ,求 ⊙O的半径;
,求 ⊙O的半径;

【答案】(1)见解析;(2)⊙O的半径为2.
【解析】试题分析:
(1)如图,连接OC,先证∠DOC=2∠BAC,结合∠PCD=2∠BAC,可得∠PCD=∠DOC;由CD⊥AB于点D可得∠DOC+∠DCO=90°,由此可得∠PCD+∠DCO=∠PCO=90°,从而可得PC是⊙O的切线;
(2)设⊙O的半径为![]() 则,OC=OB=
则,OC=OB= ![]() ,OP=AB+AP=
,OP=AB+AP= ![]() ,在Rt△OCP中,由勾股定理可得OC2+PC2=OP2,即
,在Rt△OCP中,由勾股定理可得OC2+PC2=OP2,即![]() ,解此方程即可求得⊙O的半径.
,解此方程即可求得⊙O的半径.

试题解析:
(1)如图,连接OC,
∵OC=OA,
∴∠BAC=∠ACO,
∴∠POC=∠BAC+∠ACO=2∠BAC,
又∵∠PCD=2∠BAC,
∴∠POC=∠PCD,
∵CD⊥AB于点D,
∴∠ODC=90.
∴∠POC+∠OCD=90.
∴∠PCD+∠OCD=90.
∴∠OCP=90.
∴半径OC⊥CP.
∴OP为⊙O的切线.
(2)设⊙O的半径为r,则OC=OB= ![]() ,OP=AB+AP=
,OP=AB+AP= ![]() ,
,
∵在Rt△OCP中,OC2+CP2=OP2,CP=![]()
∴![]()
解得: ![]() .
.
∴⊙O的半径为2.

【题目】阅读并解决问题:有趣的勾股数组
定义:一般地,若三角形三边长![]() ,
,![]() ,
,![]() 都是正整数,且满足
都是正整数,且满足![]() ,那么数组
,那么数组![]() 称为勾股数组.
称为勾股数组.
关于勾股数组的研究我国历史上有过非常辉煌的成就,根据我国古代数学书《周髀算经》记载,在约公元前1100年,人们就已经知道“勾广三,股修四,径隅五”(古人把较短的直角边称为勾,较长直角边称为股,而斜边则成称为弦),即知道了勾股数组![]() ,后来人们发现并证明了勾股定理.
,后来人们发现并证明了勾股定理.
公元263年魏朝刘徽注《九章算术》,文中除提到勾股数组![]() 以外,还提到
以外,还提到![]() ,
,![]() ,
,![]() ,
,![]() 等勾股数组.
等勾股数组.
设![]() ,
,![]() 是两个正整数,且
是两个正整数,且![]() ,三角形三边长
,三角形三边长![]() ,
,![]() ,
,![]() 都是正整数.
都是正整数.
下表中的![]() ,
,![]() ,
,![]() 可以组成一些有规律的勾股数组
可以组成一些有规律的勾股数组![]() :
:
|
|
|
|
|
2 | 1 | 3 | 4 | 5 |
3 | 2 | 5 | 12 | 13 |
4 | 1 | 15 | 8 | 17 |
4 | 3 | 7 | 24 | 25 |
5 | 2 | 21 | 20 | 29 |
5 | 4 | 9 | 40 | 41 |
6 | 1 | 35 | 12 | 37 |
6 | 5 | 11 | 60 | 61 |
7 | 2 | 45 | 28 | 53 |
7 | 4 | 33 | 56 | 65 |
7 | 6 | 13 | 84 | 85 |
请你仔细观察这个表格,解答下列问题:
(1)表中![]() 和
和![]() ,
,![]() 的等量关系式是________;
的等量关系式是________;
(2)表中的勾股数组用只含![]() ,
,![]() 的代数式表示为________;
的代数式表示为________;
(3)小明通过研究表中数据发现:若勾股数组中,弦与股的差为1,则勾股数的形式可表述为![]() (
(![]() ,
,![]() 为正整数),请你用含
为正整数),请你用含![]() 的代数式表示
的代数式表示![]() .
.