题目内容
【题目】如图,在![]() 中,已知
中,已知![]() 于点
于点![]() 于点
于点![]() ,
,![]() 为
为![]() 边的中点,连接
边的中点,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() 为等边三角形;④当
为等边三角形;④当![]() 时,
时,![]() .其中正确的是____________(填写序号).
.其中正确的是____________(填写序号).

【答案】①②③④
【解析】
根据直角三角形斜边上的中线等于斜边的一半可判断①②正确;
先根据直角三角形两锐角互余的性质求出∠ABM=∠ACN=30°,再根据三角形的内角和定理求出∠BCN+∠CBM=60°,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPN+∠CPM=120°,从而得到∠MPN=60°,又由①得PM=PN,根据有一个角是60°的等腰三角形是等边三角形可判断③正确;
当∠ABC=45°时,∠BCN=45°,由P为BC边的中点,得出BN=![]() PB=
PB=![]() PC,判断④正确.
PC,判断④正确.
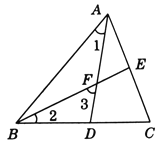
∵BM⊥AC于点M,CN⊥AB于点N,P为BC边的中点,
∴PM=![]() BC,PN=
BC,PN=![]() BC,
BC,
∴![]() ,PM=PN,①②正确;
,PM=PN,①②正确;
∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,
∴∠ABM=∠ACN=30°,
在△ABC中,∠BCN+∠CBM=180°-60°-30°×2=60°,
∵点P是BC的中点,BM⊥AC,CN⊥AB,
∴PM=PN=PB=PC,
∴∠BPN=2∠BCN,∠CPM=2∠CBM,
∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°,
∴∠MPN=60°,
∴△PMN是等边三角形,③正确;
当∠ABC=45°时,∵CN⊥AB于点N,
∴∠BNC=90°,∠BCN=45°,
∴BN=CN,
∵P为BC边的中点,
∴PN⊥BC,△BPN为等腰直角三角形,
∴BN=![]() PB=
PB=![]() PC,
PC,
∴![]() ,④正确.
,④正确.
故答案为:①②③④.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目