题目内容
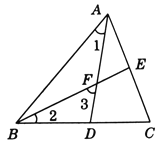
【题目】如图,∠ABC=60°,∠1=∠2.
(1)求∠3的度数;
(2)若AD⊥BC,AF=6,求DF的长.
【答案】(1)60°;(2)3
【解析】
(1)由三角形的外角性质,得到∠3=∠1+∠ABF,由∠1=∠2,得到∠3=∠ABC,即可得到答案;
(2)由(1)∠3=∠ABC=60°,由AD⊥BC,则∠2=∠1=30°,则∠ABF=30°=∠1,则BF=AF=6,即可求出DF的长度.
解:(1)根据题意,由三角形的外角性质,得
∠3=∠1+∠ABF,
∵∠1=∠2,
∴∠3=∠2+∠ABF,
∵∠ABC=∠ABF+∠2=60°,
∴∠3=60°;
(2)由(1)可知,∠3=60°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠2=30°,
∴![]() ,
,
∵∠3=∠2+∠ABF,
∴∠ABF=30°,
∵∠1=∠2=30°,
∴∠ABF=∠1=30°,
∴BF=AF=6,
∴![]() .
.

练习册系列答案
相关题目