题目内容
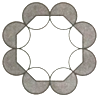
【题目】如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1 , 正八边形外侧八个扇形(阴影部分)面积之和为S2 , 则 ![]() =( )
=( )
A.![]()
B.![]()
C.![]()
D.1
【答案】B
【解析】∵正八边形的内角和为(8﹣2)×180°=6×180°=1080°,
正八边形外侧八个扇形(阴影部分)的内角和为360°×8﹣1080°=2880°﹣1080°=1800°,
∴ ![]() =
= ![]() =
= ![]() .
.
所以答案是:B.
【考点精析】通过灵活运用正多边形和圆和扇形面积计算公式,掌握圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.

练习册系列答案
相关题目