��Ŀ����
����Ŀ����������Ҫ���������⣺ 
��1���벹ȫ������ʽ��2x2��4x��0�Ľ⼯�Ĺ��� �ٹ��캯��������ͼ��
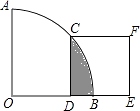
���ݲ���ʽ����������κ���y=��2x2��4x�������ߵĶԳ���x=��1���������£����㣨��1��2����x��Ľ����ǣ�0��0��������2��0���������㷨�������κ���y=��2x2��4x��ͼ����ͼ1��ʾ��
�����ν�ϣ���ý�㣺
��y=0ʱ����÷��̩�2x2��4x=0�Ľ�Ϊ��
�۽���ͼ��д���⼯��
��ͼ��ɵò���ʽ��2x2��4x��0�Ľ⼯Ϊ ��
��2�����ã�1������ʽ�⼯�ķ������裬��ʽx2��2x+1��4�Ľ⼯�� �ٹ��캯��������ͼ��
�����ν�ϣ���ý�㣻
�۽���ͼ��д���⼯��
��3����������������ʽ�⼯�Ĺ��̣�����һԪ���η��̵������ʽ��ֱ��д������x�IJ���ʽax2+bx+c��0��a��0���Ľ⼯��
���𰸡�
��1��x1=0��x2=��2����2��x��0
��2���⣺�ٹ��캯��������ͼ��
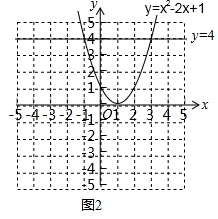
��ͼ2����
���캯��y=x2��2x+1�������ߵĶԳ���x=1��
�ҿ������ϣ��������꣨1��0����
���ڶԳ���x=1�ԳƵ�һ�Ե㣨0��1������2��1����
�����㷨����ͼ����ͼ2��ʾ��
 ��
��
�����ν�ϣ���ý�㣺
��y=4ʱ������x2��2x+1=4�Ľ�Ϊ��x1=��1��x2=3��
�۽���ͼ��д���⼯��
��ͼ2֪������ʽx2��2x+1��4�Ľ⼯�ǣ���1��x��3��
��3���⣺�ٵ�b2��4ac��0ʱ������x�IJ���ʽax2+bx+c��0��a��0��
�Ľ⼯��x�� ![]() ��x��
��x�� ![]() ��
��
��b2��4ac=0ʱ������x�IJ���ʽax2+bx+c��0��a��0���Ľ⼯�ǣ�x�٩� ![]() ��
��
��b2��4ac��0ʱ������x�IJ���ʽax2+bx+c��0��a��0���Ľ⼯��ȫ��ʵ����
���������⣺��1���ڷ��̩�2x2��4x=0�Ľ�Ϊ��x1=0��x2=��2���۲���ʽ��2x2��4x��0�Ľ⼯Ϊ����2��x��0��
�����㾫�������ڱ��⿼��Ķ��κ�����ͼ��Ͷ��κ��������ʣ���Ҫ�˽���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С���ܵó���ȷ�𰸣�

����Ŀ������Ϣ���ٷ�չ����ᣬ����Ϣ���ѡ��ѳ�Ϊ�����������Ҫ��ɲ��֣�ij��У��֯����С����֣���е�һ�����������ȡ���ּ�ͥ������ÿ��������Ϣ���ѵĽ�����������������ͼ��ʾ�IJ�����ͳ�Ʊ���ͳ��ͼ����֪A��B���黧��Ƶ��ֱ��ͼ�ĸ߶ȱ�Ϊ1��5�� ����Ϣ���Ѷ����ͳ�Ʊ�
��� | ���ѶԪ�� |
A | 10��x��100 |
B | 100��x��200 |
C | 20��x��300 |
D | 300��x��400 |
E | x��400 |
����ͼ����������ݽ���������⣺
��1����ν��ܵ����������
��2��������ͳ��ͼ�У���E������Ӧ��Բ�ĽǵĶ�������
��3�����㲹ȫƵ��ֱ��ͼ��
��4������������2000��ס�������������Ϣ���Ѷ����200Ԫ�Ļ����Ƕ��٣�
����Ŀ���ţ�2��������ίԱ�û��Ƿ�ͳ�Ʊ���40��ͬѧͶ��ʵ����ijɼ��������ͼ��ʾ������40��ͬѧͶ��ʵ����ijɼ�����������λ���ֱ��ǣ� ��
�ɼ� | 6 | 7 | 8 | 9 | 10 |
���� |
| �� | �� | �� | �� |
A.8��8
B.8��8.5
C.9��8
D.9��8.5