��Ŀ����
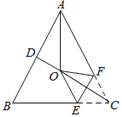
����Ŀ����ͼ1����EΪ����ABCD�ı�AD��һ�㣬��P�ӵ�B������BE��ED��DC�˶�����Cֹͣ����Q�ӵ�B������BC�˶�����Cֹͣ�������˶����ٶȶ���1cm/s������P��Qͬʱ��ʼ�˶������˶�ʱ��Ϊt��s������BPQ�����Ϊy��cm2������֪y��t֮��ĺ���ͼ����ͼ2��ʾ���������н��ۣ�����0��t��10ʱ����BPQ�ǵ��������Σ���S��ABE=48cm2����14��t��22ʱ��y=110��5t�������˶������У�ʹ����ABP�ǵ��������ε�P��һ����3����������BPQ����BEA����ʱ��t=14.5��������ȷ���۵�����ǣ�������

A. �٢ܢ� B. �٢ڢ� C. �٢ۢ� D. �٢ۢ�
���𰸡�D
��������
�������⣬�õ�P��Q�ֱ�ͬʱ����D��C���жϢ٢ڣ��ֶ�����PQλ�ú�����жϢۣ����ɵ��������εķ������۷���ȷ���ܣ���������������λ���жϵ�P��DC��ʱ��������BPQ����BEA���ƵĿ����ԣ��������ۼ��㼴�ɣ�
�⣺��ͼ���֪����Q����Cʱ����P��E��BE=BC=10��ED=4
�ʢ���ȷ
��AE=10��4=6
t=10ʱ����BPQ���������![]()
��AB=DC=8
��![]()
�ʢڴ���
��14��t��22ʱ��![]()
�ʢ���ȷ��
�ֱ���A��BΪԲ�ģ�ABΪ�뾶��Բ������Բ�������Ӽ�ΪAB��ֱƽ����
���A����B��AB��ֱƽ�������P����·���Ľ�����P��������ABP�ǵ���������
��ʱ�����������ĵ���4�����ʢܴ���
�ߡ�BEAΪֱ��������
��ֻ�е�P��DC����ʱ������BPQ����BEA����
����֪��PQ=22��t
�൱![]() ��
��![]() ʱ����BPQ����BEA����
ʱ����BPQ����BEA����
�ֱ���ֵ����
![]() ��
��![]() ��
��
���t=![]() ����ȥ����t=14.5
����ȥ����t=14.5
�ʢ���ȷ
��ѡ��D��