Question

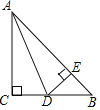
【题目】如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠BAC交BC于点D，过点D作DE⊥AB，垂足为E．

（1）求证：AC＝AE；

（2）若△BDE的周长为20，求AB的长．

Answer 1

【答案】（1）见解析；（2）AB＝20

【解析】

（1）欲证明AC＝AE，只要证明△ADC≌△ADE（AAS）即可．

（2）证明△BDE的周长＝AB即可解决问题．

（1）证明：∵AD平分∠CAB，

∴∠DAC＝∠DAE，

∵∠C＝90，DE⊥AB，

∴∠C＝∠AED＝90，

∵AD＝AD，

∴△ADC≌△ADE（AAS），

∴AC＝AE．

（2）解：∵△ADC≌△ADE，

∴AC＝AE，DE＝DC，

∵△BDE的周长＝DE+BD+BE＝20，

∴DC+DB+BE＝20，

∴BC+BE＝20，

∵BC＝AC＝AE，

∴AE+EB＝20，

∴AB＝20．