题目内容
【题目】已知,在以O为原点的直角坐标系中,抛物线的顶点为A(1,4),且经过点B(2,3),与x轴交于C、D两点.
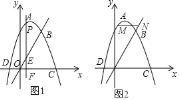
(1)求直线OB的函数表达式和该抛物线的函数表达式;
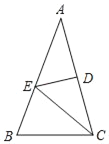
(2)如图1,点P是x轴上方的抛物线上一动点,过点P作直线PF⊥x轴于点F,交直线OB于点E.若PE=3EF,求出P点的横坐标;
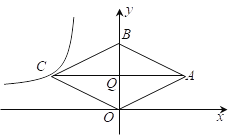
(3)如图2,点M是抛物上的一个动点,且在直线OB的上方,过点M作x轴的平行线与直线OB交于点N,T是抛物线对称轴上一点,当MN最大且△MDT周长最小时,直接写出T的坐标.
【答案】(1) y=x2﹣2x+5;(2) P点的横坐标为4﹣![]() ; (3) T的坐标为(1,3).
; (3) T的坐标为(1,3).
【解析】
(1)由B点坐标利用待定系数法可求直线OB解析式,利用顶点式可求得抛物线解析式;
(2)设P(x,x2-2x+5),则可表示出E点坐标,由PE=3EF可得到方程解答即可;
(3)当M与B关于抛物线的对称轴对称时,MN最大,进而得出T的坐标.
(1)设直线OB解析式为y=kx,由题意可得3=2k,解得k=1.5,
∴直线OB解析式为y=1.5x,
∵抛物线顶点坐标为(1,4),
∴可设抛物线解析式为y=a(x﹣1)2+4,
∵抛物线经过B(2,3),
∴3=a+4,解得a=1,
∴抛物线为y=x2﹣2x+5;
(2)设P(x,x2﹣2x+5),E点坐标为(x,1.5x),
∵PE=3EF,
∴x2﹣2x+5=4×1.5x,
解得:![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
P点的横坐标为4﹣![]() .
.
(3)当M与B关于抛物线的对称轴对称时,MN最大,此时B与N重合,
此时M的坐标为(0,3),
当MT垂直对称轴时,△MDT周长最小,
此时T的坐标为(1,3).

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目