题目内容
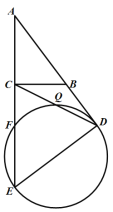
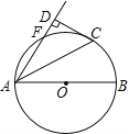
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且点C为弧BF的中点,连接AC、AF,过点C作CD⊥AF交AF延长线于点D.
(1)求证:CD是⊙O的切线;
(2)判断线段AB、AF与AD之间的数量关系,并说明理由.
【答案】(1)证明见解析;(2)AF+AB=2AD ,理由见解析.
【解析】
(1)由![]() =
=![]() ,OA=OC知∠DAC=∠BAC=∠ACO,由CD⊥AF知∠DAC+∠DCA=90°,从而得∠DCO=90°,从而得证;
,OA=OC知∠DAC=∠BAC=∠ACO,由CD⊥AF知∠DAC+∠DCA=90°,从而得∠DCO=90°,从而得证;
(2)作CE⊥AB,连接CF,CB,先证Rt△DAC≌Rt△EAC得AD=AE,再证Rt△CDF≌Rt△CEB得DF=EB,根据AF=AD﹣CF,AB=AE+BE可得答案.
(1)连接OC.
∵![]() =
=![]() ,OA=OC,∴∠DAC=∠BAC=∠ACO.
,OA=OC,∴∠DAC=∠BAC=∠ACO.
∵CD⊥AF于D,∴∠DAC+∠DCA=90°,∴∠DCA+∠OCA=90°,即∠DCO=90°,∴CD为⊙O的切线.
(2)AF+AB=2AD.理由如下:
过C点作CE⊥AB于E,连接CF,CB,则∠CDA=∠CEA=90°.
∵∠DAC=∠EAC,AC=AC,∴Rt△DAC≌Rt△EAC(AAS),CD=CE,AD=AE.
又∵∠DFC+∠AFC=180°,∠AFC+∠B=180°,∴∠DFC=∠B,∴Rt△CDF≌Rt△CEB(AAS),∴DF=EB,∴AF=AD﹣CF,AB=AE+BE,∴AF+AB=AD+AE=2AD.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目