题目内容
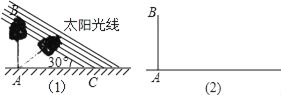
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时相向匀速行驶,当乙车到达
两地同时相向匀速行驶,当乙车到达![]() 地后,继续保持原速向远离
地后,继续保持原速向远离![]() 的方向行驶,而甲车到达
的方向行驶,而甲车到达![]() 地后,休息半小时后立即掉头,并以原速的
地后,休息半小时后立即掉头,并以原速的![]() 倍与乙车同向行驶,经过一段时间后,两车先后到达距
倍与乙车同向行驶,经过一段时间后,两车先后到达距![]() 地
地![]() 的
的![]() 地并停下来,设两车行驶的时间为
地并停下来,设两车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,
,![]() 与
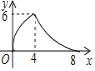
与![]() 的函数关系如图,则当甲车从
的函数关系如图,则当甲车从![]() 地掉头追到乙车时,乙车距离
地掉头追到乙车时,乙车距离![]() 地__________
地__________![]() .
.
【答案】160
【解析】
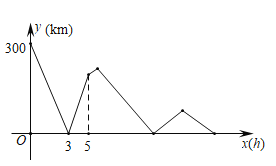
当x=0时,y=300,由此可得AB两地的距离为300km,由图象可知甲车到达B地用5小时,3小时后两车相遇,从而可求甲车的速度以及两车的速度之和,进而可得乙车的速度,再根据乙行驶5.5小时后,甲车从B地掉头追乙车,根据速度差可求出追乙车所用的时间,然后即可求解.
解:由图象可得:当x=0时,y=300,
∴AB=300千米,
∴甲车的速度=300÷5=60千米/小时,
又∵300÷3=100千米/小时,
∴乙车的速度=10060=40千米/小时,
∴当甲车从B地掉头开始追乙车时,乙车行驶的距离为40×5.5=220km,
∴甲车从B地掉头到追上乙车用的时间为:220÷(60×![]() -40)=5.5小时,
-40)=5.5小时,
∴当甲车从![]() 地掉头追到乙车时,乙车距离
地掉头追到乙车时,乙车距离![]() 地600-40×(5.5+5.5)=160km,
地600-40×(5.5+5.5)=160km,
故答案为:160.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目