题目内容
【题目】已知点A,B在数轴上分别表示m,n,其中m<n.
(1)填写下表;
m | 3 | ﹣6 | ﹣5 |
n | 5 | 4 | ﹣4 |
A,B两点的距离 |
|
|
|
(2)若A,B两点的距离为d,则d与m,n的数量关系为 ;
(3)若S=|x﹣3|+|x﹣4|+|x﹣5|+…+|x﹣2018|,求S的最小值,并写出当S取最小值时x的取值范围.
【答案】(1)2,10,1;(2)d=|n﹣m|;(3)1088064.1010≤x≤1011
【解析】
(1)结合点在数轴上的位置进行计算;
(2)根据(1)即可发现规律:数轴上两点间的距离等于表示两个点的数的差的绝对值,或直接让较大的数减去较小的数;
(3)利用S=|x﹣3|+|x﹣4|+|x﹣5|+…+|x﹣2018|是数轴上点x 与 3、4、5、…2018的距离和,进而得出当1010≤x≤1011 时,S最小求出即可.
(1)填写下表;
m | 3 | ﹣6 | ﹣5 |
n | 5 | 4 | ﹣4 |
A,B两点的距离 | 2 | 10 | 1 |
故答案为:2,10,1;
(2)d=n﹣m,
故答案为:d=n﹣m;
(3)根据绝对值的几何意义,|x﹣a|的意义是数轴上表示数x的点到表示数a的点之间的距离.
s=|x﹣3|
当x=3时,s有最小值s=0
s=|x﹣3|+|x﹣4|
当3≤x≤4 时,s有最小值s=4﹣3=1
s=|x﹣3|+|x﹣4|+|x﹣5|
当x=4时,S有最小值S=2
s=|x﹣3|+|x﹣4|+|x﹣5|+|x﹣6|
当4≤x≤5 时,S有最小值S=(6﹣3)+(5﹣4)=3+1=4
s=|x﹣3|+|x﹣4+|x﹣5|+|x﹣6|+|x﹣7|
当x=5时,S有最小值S=(7﹣3)+(6﹣4)+0=4+2=6,
…
根据观察所得规律
|x﹣3|+|x﹣4|+|x﹣5|+…+|x﹣2018|共有(2018﹣3)+1=2016项
(2018+3)÷2=1010.5,
∴1010≤x≤1011,
当1010≤x≤1011时,S有最小值,
S=(2018﹣3)+(2017﹣4)+(2016﹣5)+…(1011﹣1010)
=2015+2013+2011+…+1
=![]() (2015+1)×1008
(2015+1)×1008
=1088064.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】今年“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数,单位:万人),已知9月30日的游客人数为0.3万人,请回答下列问题:
日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 | +1.8 | +0.8 | +0.2 | -0.4 | -0.8 | +0.2 | -1.0 |
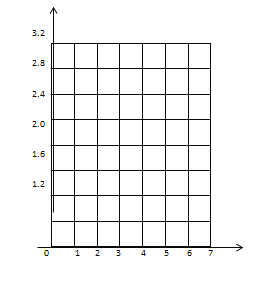
(1)七天内游客人数最多的是 日,最少的是 日;
(2)若以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数变化情况?
(3)求这7天的游客人数是多少万人.