题目内容
【题目】综合实践
问题情景:某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
操作探究:
⑴若准备制作一个无盖的正方体形纸盒,如图1,下面的哪个图形经过折叠能围成无盖正方体形纸盒?

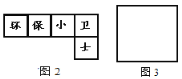
⑵如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?
⑶如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.
①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.
②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高为 cm,底面积为 cm2,当小正方形边长为4cm时,纸盒的容积为 cm3.
【答案】(1)C;(2)卫;(3)①答案见解析;②x,(20﹣2x)2,576.
【解析】
(1)由平面图形的折叠及正方体的展开图解答本题;
(2)正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,据此作答;
(3)①根据题意,画出图形即可;
②根据正方体底面积、体积,即可解答.
(1)A.有田字,故A不能折叠成无盖正方体;
B.只有4个小正方形,无盖的应该有5个小正方形,不能折叠成无盖正方体;
C.可以折叠成无盖正方体;
D.有6个小正方形,无盖的应该有5个小正方形,不能折叠成无盖正方体.
故选C.
(2)正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,所以与“保”字相对的字是“卫”.
(3)①如图,
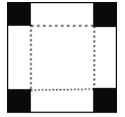
②设剪去的小正方形的边长为x(cm),用含字母x的式子表示这个盒子的高为xcm,底面积为(20﹣2x)2cm2,当小正方形边长为4cm时,纸盒的容积为=x(20﹣2x)2=4×(20﹣2×4)2=576(cm3).
故答案为:x,(20﹣2x)2,576.

 阅读快车系列答案
阅读快车系列答案【题目】已知点A,B在数轴上分别表示m,n,其中m<n.
(1)填写下表;
m | 3 | ﹣6 | ﹣5 |
n | 5 | 4 | ﹣4 |
A,B两点的距离 |
|
|
|
(2)若A,B两点的距离为d,则d与m,n的数量关系为 ;
(3)若S=|x﹣3|+|x﹣4|+|x﹣5|+…+|x﹣2018|,求S的最小值,并写出当S取最小值时x的取值范围.