题目内容
【题目】如图是墙壁上在![]() ,
,![]() 两条平行线间的边长为
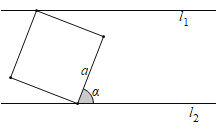
两条平行线间的边长为![]() 的正方形瓷砖,该瓷砖与平行线的较大夹角为
的正方形瓷砖,该瓷砖与平行线的较大夹角为![]() ,则两条平行线间的距离为( )
,则两条平行线间的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
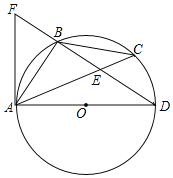
如图,过B作EF⊥l1于点E,EF与l2交于点F,则EF⊥l2,证明△ABE≌△BCF,得BE=CF,解Rt△BCF便可得结果.
解:如图,过B作EF⊥l1于点E,EF与l2交于点F,则EF⊥l2,
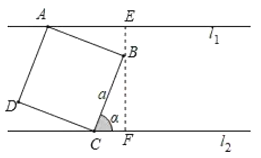
∵四边形ABCD是正方形,
∴AB=BC=a,∠ABC=90°,
∴∠ABE+∠CBF=∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
∵∠AEB=∠BFC=90°,
∴△ABE≌△BCF(AAS),
∴BE=CF,
在Rt△BCF中,BF=asinα,CF=acosα,
∴BE=acosα,
∴EF=BE+BF=asinα+acosα,
即两条平行线间的距离为asinα+acosα,
故选:B.

练习册系列答案
相关题目
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
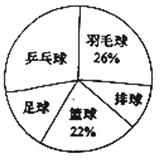
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.