Question

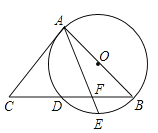
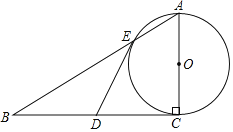
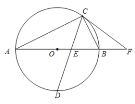
【题目】如图，AB是⊙O的直径，点C是圆上一点，点D是半圆的中点，连接CD交OB于点E，点F是AB延长线上一点，CF＝EF．

（1）求证：FC是⊙O的切线；

（2）若CF＝5，，求⊙O半径的长．

Answer 1

【答案】（1）证明见解析；（2）AO＝.

【解析】

（1）连接OD，利用点D是半圆的中点得出∠AOD与∠BOD是直角，之后通过等量代换进一步得出∠FCE+∠OCD=∠OED+∠ODC=90°从而证明结论即可；

（2）通过得出＝，再证明△ACF∽△CBF从而得出AF＝10，之后进一步求解即可.

证明：连接OD，

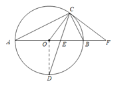
∵点D是半圆的中点，

∴∠AOD=∠BOD=90°.

∴∠ODC+∠OED=90°.

∵OD=OC，

∴∠ODC=∠OCD.

又∵CF=EF，

∴∠FCE=∠FEC.

∵∠FEC=∠OED，

∴∠FCE=∠OED.

∴∠FCE+∠OCD=∠OED+∠ODC=90°.

即FC⊥OC.

∴FC是⊙O的切线.

（2）∵tanA＝，

∴在Rt△ABC中，＝.

∵∠ACB＝∠OCF＝90°，

∴∠ACO＝∠BCF＝∠A.

∴△ACF∽△CBF，

∴＝＝＝.

∴AF＝10.

∴CF2＝BF·AF.

∴BF＝.

∴AO＝＝.