题目内容
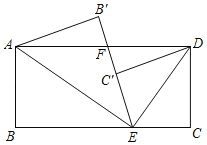
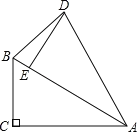
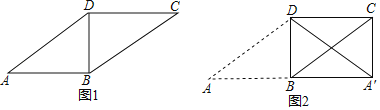
【题目】如图1,在平行四边形ABCD中,对角线BD⊥AB,以BD为对称轴将△ABD翻折,点A的对应点为A′,连接A′C,得到图2.
推理证明
(1)求证:四边形A′BDC是矩形;
实践操作
(2)在图1中将△ABD或△BDC进行平移、旋转或轴对称变换,重新构造一个特殊四边形.
要求:①画出图形,标明字母;②写出构图过程及构造的特殊四边形的名称.(不要求证明)
【答案】(1)证明见解析;(2)见解析.
【解析】
(1)根据平行四边形的性质,可得AB与DC,AD与BC的关系,根据轴对称的性质,可得BD⊥AB,A′B=AB,根据矩形的判定,可得答案;
(2)根据平移的性质,平行四边形的判定,可得答案.
(1)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD=BC.
又∵△ABD与△A′BD关于BD对称,BD⊥AB,
∴A′B=AB=DC,A′B∥DC,
∴四边形A′BDC是平行四边形,
∵A′D=AD,
∴A′D=BC,
∴四边形A′BDC是矩形;
(2)答案不唯一,如:如图,将△BCD沿DA方向平移,得到△D′B′C′,
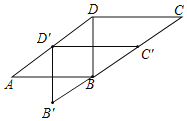
由平移可得,DD′∥BB′且DD′=BB′,
∴四边形DD′B′B是平行四边形.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目