题目内容
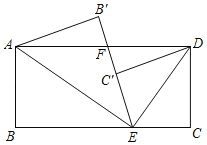
【题目】如图所示,在矩形ABCD中,AB=1,在线段BC上取一点E,连接AE、ED,将△ABE沿AE翻折,使点B落在B'处,线段EB'交AD于点F.将△ECD沿DE翻折,使点C的对应点C'落在线段EB'上,且点C'恰好为EB'的中点,则线段EF的长为_____.
【答案】![]()
【解析】
由折叠的性质可得AB=AB'=CD=C'D=1,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,由中点性质可得B'E=2C'E,可得BC=AD=3EC,由勾股定理可求可求CE的长,由“AAS”可证△AB'F≌△DC'F,可得C'F=B'F=![]() ,即可求解.
,即可求解.
∵四边形ABCD是矩形,
∴AB=CD=1,AD=BC,∠B=∠C=90°
由折叠的性质可得:AB=AB'=CD=C'D=1,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,
∵点C'恰好为EB'的中点,
∴B'E=2C'E,
∴BE=2CE,
∴BC=AD=3EC,
∵AE2=AB2+BE2,DE2=DC2+CE2,AD2=AE2+DE2,
∴1+4CE2+1+CE2=9CE2,
∴CE=![]() ,
,
∴B'E=BE=![]() ,BC=AD=
,BC=AD=![]() ,C'E=
,C'E=![]() ,
,
∴B'C'=![]() ,
,
∵∠B'=∠DC'F=90°,∠AFB'=∠DFC',AB'=C'D,
∴△AB'F≌△DC'F(AAS),
∴C'F=B'F=![]() ,
,
∴EF=C'E+C'F=![]() ,
,
故答案为:![]()

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
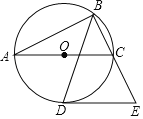
双基同步导航训练系列答案【题目】如图,以△ABC的边AC为直径的O恰为△ABC的外接圆,∠ABC的平分线交O于点D,过点D作DE∥AC交BC的延长线于点E
(1)求证:DE是⊙O的切线;
(2)若AB=4![]() ,BC=2
,BC=2![]() ,求DE的长.
,求DE的长.
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
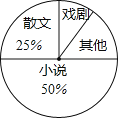
(1)计算m= ;
(2)在扇形统计图中,“其他”类所占的百分比为 ;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.