题目内容
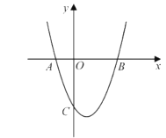
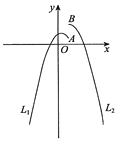
【题目】如图,函数y=-x2+![]() x+c(-2020≤x≤1)的图象记为L1,最大值为M1;函数y=-x2+2cx+1(1≤x≤2020)的图象记为L2,最大值为M2.L1的右端点为A,L2的左端点为B,L1,L2合起来的图形记为L.
x+c(-2020≤x≤1)的图象记为L1,最大值为M1;函数y=-x2+2cx+1(1≤x≤2020)的图象记为L2,最大值为M2.L1的右端点为A,L2的左端点为B,L1,L2合起来的图形记为L.
(1)当c=1时,求M1,M2的值;
(2)若把横、纵坐标都是整数的点称为“美点”,当点A,B重合时,求L上“美点”的个数;
(3)若M1,M2的差为![]() ,直接写出c的值.
,直接写出c的值.
【答案】(1)当c=1时,M1=![]() ,M2=2;(2)3030;(3)c=-
,M2=2;(2)3030;(3)c=-![]() 或2.
或2.
【解析】
(1)当c=1时,把函数的解析式化成顶点式即可求得![]() ,
,![]() 的值;
的值;
(2)由已知可得点A,B重合时,![]() ,
,![]() ,L1上有1011个“美点”,L2上有2020个“美点”.则L上“美点”的个数是1011+2020-1=3030;
,L1上有1011个“美点”,L2上有2020个“美点”.则L上“美点”的个数是1011+2020-1=3030;
(3)当![]() 时,
时,![]() ,由于L2的对称轴为
,由于L2的对称轴为![]() ,分两种情况求解:当c≥1时,
,分两种情况求解:当c≥1时,![]() =c2+1;当c<1时,
=c2+1;当c<1时,![]() =2c;再由已知列出等式即可求c的值.
=2c;再由已知列出等式即可求c的值.
(1)当c=1时,
函数y=-x2+![]() x+c=-x2+
x+c=-x2+![]() x+1=-(x-
x+1=-(x-![]() )2+
)2+![]() ,
,
又-2020≤x≤1,
∴M1=![]() ,
,
y=-x2+2cx+1=-x2+2x+1=-(x-1)2+2,
又1≤x≤2020,
∴M2=2.
(2)当x=1时,y=-x2+![]() x+c=c-
x+c=c-![]() ;y=-x2+2cx+1=2c.
;y=-x2+2cx+1=2c.
若点A,B重合,则c-![]() =2c,c=-
=2c,c=-![]() ,
,
∴L1∶y=-x2+![]() x-
x-![]() (-2020≤x≤1);
(-2020≤x≤1);
L2∶y=-x2-x+1(1≤x≤2020).
在L1上,x为奇数的点是“美点”,则L1上有1011个“美点”;
在L2上,x为整数的点是“美点”,则L2上有2020个“美点”.
又点A,B重合,
则L上“美点”的个数是1011+2020-1=3030;
(3)y=-x2+![]() x+c(-2020≤x≤1)上时,当
x+c(-2020≤x≤1)上时,当![]() 时,
时,![]() ,
,
y=-x2+2cx+1(1≤x≤2020),对称轴为![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() (舍去)或
(舍去)或![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() (舍去)或
(舍去)或![]() ;
;
综上,![]() 或
或![]() .
.