题目内容
【题目】如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)

【答案】巡逻艇能在1小时内到达渔船C处.
【解析】
由已知可得△ABC中∠C=67°,∠B=37°且AB=20海里.要求BC的长,可以过A作AD⊥BC于D,先求出CD和BD的长,就可转化为运用三角函数解直角三角形.
过点A作AH⊥BC,垂足为点H.
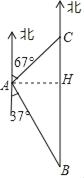
由题意,得∠ACH=67°,∠B=37°,AB=20.
在Rt△ABH中,
∵sinB=![]() ,∴AH=ABsin∠B=20×sin37°≈12,
,∴AH=ABsin∠B=20×sin37°≈12,
∵cosB=![]() ,∴BH=ABcos∠B=20×cos37°≈16,
,∴BH=ABcos∠B=20×cos37°≈16,
在Rt△ACH中,
∵![]() ,
,
∴CH=![]() ,
,
∵BC=BH+CH,∴BC≈16+5=21.
∵21÷25<1,
所以,巡逻艇能在1小时内到达渔船C处.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目