题目内容

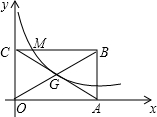
如图，矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上，OA=4，OC=2，G为矩形对角线的交点，经过点G的双曲线y=
k
x
与BC相交于点M，则CM：MB=______．
∵G为矩形OABC对角线的交点，
而，OA=4，OC=2，
∴G的坐标为（2，1），
∴k=2，
∴y=
2
x
，
∵双曲线y=
k
x
与BC相交于点M，
∴M的纵坐标是2，
∴纵坐标y=1，
∴CM=1，
MB=3，
∴CM：MB=1：3．
故答案为：1：3．
练习册系列答案
相关题目
已知如图，△AOB的OB边在x轴上，∠OAB=90°，OA=AB=3
2
，反比例函数y1=
k
x
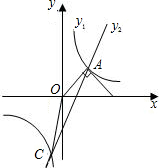过A点，一次函数y2=ax-b的图象过A点且与反比例函数图象的另一交点为C（-1，m），连接OC
（1）求出反比例函数与一次函数的解析式；
（2）求△OAC的面积；
（3）根据图象，直接写出当y1≥y2时，x的取值范围．
如图，在平面直角坐标系中，函数y=
k
x
（x＞0常数k＞0）的图象经过点A（1，2），B（m，n）（m＞1），过点B作y轴的垂线，垂足为C，若△ABC面积为2，求点B的坐标______．
直线l经过A（1，0）且与双曲线y=
m
x
(x＞0)在第一象限交于点B（2，1），过点P（p+1，p-1）（p＞1）作x轴的平行线分别交于双曲线y=
m
x
(x＞0)和y=-
m
x
（x＜0）于M，N两点，
（1）求m的值及直线l的解析式；
（2）直线y=-x-3与x轴、y轴分别交于点C、D，点E在直线y=-x-3上，且点E在第三象限，使得
CE
ED
=2，平移线段ED得线段HQ（点E与H对应，点D与Q对应），使得H、Q恰好都落在y=
m
x
的图象上，求H、Q两点坐标．
（3）是否存在实数p，使得S△AMN=4S△APM？若存在，求所有满足条件的p的值，若不存在，请说明理由．
已知质量一定的某物体的体积V（m3）是密度ρ（kg/m3）的反比例函数，其图象如图所示：
（1）请写出该物体的体积V与密度ρ的函数关系式；
（2）当该物体的密度ρ=3.2Kg/m3时，它的体积v是多少？
（3）如果将该物体的体积控制在10m3～40m3之间，那么该物体的密度应在什么范围内变化？
如图所示，反比例函数y=
k
x
的图象经过点A（-
3
，b），过点A作AB垂直x轴于点B，△AOB的面积为
3
．
（1）求k和b的值；
（2）若一次函数y=ax+1的图象经过点A，并且与x轴相交于点M，求△AOM的面积．
如图，正方形ABCD的边AB在x轴的正半轴上，C（2，1），D（1，1）．反比例函数y=
k
x
的图象与边BC交于点E，与边CD交于点F．已知BE：CE=3：1，则DF：FC等于（　　）
A．4：1B．3：1C．2：1D．1：1
如图，若反比例函数y=-
8
x
与一次函数y=mx-2的图象都经过点A（a，2）
（1）求A点的坐标及一次函数的解析式；
（2）设一次函数与反比例函数图象的另一交点为B，求B点坐标，并利用函数图象写出使一次函数的值小于反比例函数的值的x的取值范围．
对某校九年级随机抽取若干名学生进行体能测试，成绩记为1分，2分，3分，4分共4个等级，将调查结果绘制成如下条形统计图（图1）和扇形统计图（图2）．根据图中信息，这些学生的平均分数是______分．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网