题目内容
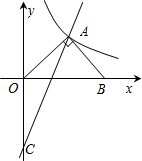
已知如图,△AOB的OB边在x轴上,∠OAB=90°,OA=AB=3
,反比例函数y1=
过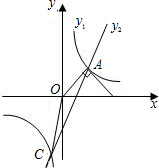 A点,一次函数y2=ax-b的图象过A点且与反比例函数图象的另一交点为C(-1,m),连接OC
A点,一次函数y2=ax-b的图象过A点且与反比例函数图象的另一交点为C(-1,m),连接OC
(1)求出反比例函数与一次函数的解析式;
(2)求△OAC的面积;
(3)根据图象,直接写出当y1≥y2时,x的取值范围.
| 2 |
| k |
| x |
 A点,一次函数y2=ax-b的图象过A点且与反比例函数图象的另一交点为C(-1,m),连接OC
A点,一次函数y2=ax-b的图象过A点且与反比例函数图象的另一交点为C(-1,m),连接OC(1)求出反比例函数与一次函数的解析式;
(2)求△OAC的面积;
(3)根据图象,直接写出当y1≥y2时,x的取值范围.
(1)设A(x,y)在△AOB中,∠OAB=90°且OA=AB=3
所以x=y=sin45°×OA=3
将点A(3,3)代入反比例函数y1=
中得3=
,k=9
又∵点C(-1,m)在反比例函数y1=
上
∴m=-9
又∵点A(3,3),点C(-1,-9)在直线y2=ax-b上
∴
解得a=3,b=6
∴该反比例函数的解析式为:y1=
,
一次函数的解析式为:y2=3x-6
(2)由(1)得点A(3,3),点C(-1,-9),AC=
=4
点O(0,0)到直线y2=3x-6的距离h=
=
所以△OAC的面积S=
×4
×
=12
(3)如图所示,y1≥y2,即
≥3x-6
当x>0,要使y1≥y2时,x的取值范围为:(0<x≤1+
)
当x<0,要使y1≥y2时,x的取值范围为:(x≤1-
)
| 2 |
所以x=y=sin45°×OA=3
将点A(3,3)代入反比例函数y1=
| k |
| x |
| k |
| 3 |
又∵点C(-1,m)在反比例函数y1=
| 9 |
| x |
∴m=-9
又∵点A(3,3),点C(-1,-9)在直线y2=ax-b上
∴
|
∴该反比例函数的解析式为:y1=
| 9 |
| x |
一次函数的解析式为:y2=3x-6
(2)由(1)得点A(3,3),点C(-1,-9),AC=
| (3+1)2+(3+9)2 |
| 10 |
点O(0,0)到直线y2=3x-6的距离h=
| 6 | ||
|
| 6 | ||
|
所以△OAC的面积S=
| 1 |
| 2 |
| 10 |
| 6 | ||
|
(3)如图所示,y1≥y2,即
| 9 |
| x |
当x>0,要使y1≥y2时,x的取值范围为:(0<x≤1+
| 2 |
当x<0,要使y1≥y2时,x的取值范围为:(x≤1-
| 2 |

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 别作x轴的垂线,与双曲线y=
别作x轴的垂线,与双曲线y=